Question

Nature of the decimal expansion of rational numbers

Explanation

Decimal Expansion of Rational Number

In this chapter, we will study the decimal expansion of rational numbers. Students would be able to get the right understanding of the expansion of rational numbers. Before we discuss the representation of the decimal expansion of rational numbers, we should first try to understand what is a rational number. Numbers that can be presented in the form of p/q where p and q are integers and q ≠ 0 are termed as rational numbers. Here, the numbers which are simplified further, they result in decimals. We will now learn how to expand such decimals. For example, 5, -7.2, 2/3 are some examples of rational numbers.

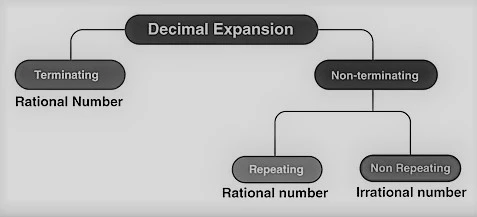
We can try to consider the number of 44.4444 which happens to be a rational number. It can be represented in the form of 100/4. We can see that the decimal part .444 proves to be the non-terminating repeating part for which it is termed as a recurring decimal number.

Let us consider any decimal number. E.g., 0.456. We can try to write it as 456/1000 or 456/10³ Similarly, we can write the numbers, 0.5543 and 0.045 and .56 as 5543/10⁴, 45/10^3, and 56/10² respectively in the fractional form. So, it can be said that any decimal number that has denominator in powers of 10 can be represented as a fraction. We are quite familiar that the prime factors of 10 are 2 and 5 where it can be said that it can be represented by p/q where co-primes are p and q and the prime factorization of q is of the form 2^x 5^y assuming that both x and y are non-negative integers.

Theorem 1: If m proves to be any rational number whose decimal expansion is terminating in nature, then m can be expressed in the form of pq, where p and q are co-primes, and the prime factorization of q is of the form 2x 5y, where x and y are non-negative integers.

The converse of this theorem is also true, and it can be stated as follows:

Theorem 2: If m is a rational number, which can be represented as the ratio of two integers, i.e. pq and the prime factorization of q takes the form 2x 5y, where both x and y are non-negative integers then, it can be said that x has a decimal expansion which proves to be terminating.

Consider the following examples:

1. 7/8  = 7/2³ = 7 x 5³/2³ x 5³   = 875/10


2. 3/80 =  3 / 2⁴ x 5 = 3 x 5³ / 2⁴ x 5⁴ = 375

Theorem 3: If m is a rational number, which can be represented as the ratio of two integers i.e. pq and the prime factorization of q does not takes the form 2x 5y, where both x and y are considered to be non-negative integers. Then, we can say that x has a decimal expansion which is non-terminating repeating (recurring).

Consider the following examples:

1. 1/6 = 0.1666…. = 0.16 ̇


2. 7/12 = 0.58333… = 0.583


3. 9/11 = 0.818= 0.81

Related Videos:

• Divisibility


• What is Euclid Division?


• Euclid Division lemma


• Euclid division algorithm


• Proof of Euclid division lemma

Solved Examples Decimal Expansion

Example 1: Can you convert the following into a rational form: x=0.343434...

Solution: Given,

x=0.343434

⇒100x=34.343434…

By subtracting these two, we have,

99x=34

Or, x = 34/99

Example 2: Can you convert the following into a rational form: y=1.721873873873...

Solution: Given,

y=1.721873873873...

By multiplying by 1000 and 1000000, we get,

⇒1000y=1721.873873873…

⇒ 1000000y=1721873.873873873...

By subtracting these two, we have,

(1000000−1000)y=1721873−1721

⇒999000y=1720152

⇒ 1720152/999000

Example 3:  Can you express the following decimal expression into rational numbers.

(i) 0.24 (bar)

Solution:

Let x = 0.242424............  -----(1)

We have the sign bar for two digits, for which we have to multiply (1) by 100 on both sides.

So, 100x =  24.2424...........------(2)

(2) - (1)  

100x - x =24.2424......-0.2424...........

99x = 24

x = 24/99

x  = 8/33

Therefore the rational form of the given decimal is 8/33.

(ii)  2.327 (bar)

Solution:

Let x =  2.327327............ -----(1)

We have the sign bar for three digits for which we have to multiply (1) by 1000 on both sides.

So, 1000x = 2327.327327...........------(2)

(2) - (1)  

1000x - x = 2327.327327.....-2.327327........

999x = 2325

So, x = 2325/999

x =  775/333

Therefore, the rational form of the given decimal is 775/333.

(iii)  -5.132

Solution:

We can find that the given decimal is terminating decimal. After the decimal, there are three digits. So, in this case, we have to multiply the numerator and denominator by 1000.

So, -5.132 = -5132/1000

  = -2566/500

  = -1283/250

(iv) 3.17 (bar) (the bar is only for 7)

Solution :

Let x = 3.177777...........  -----(1)

As we have got the sign bar for only one digit, so here we need to multiply (1) by 10 on both sides.

So, 10x = 31.77777...........------(2)

Now, by (2) - (1)  

10x - x = 31.7777.....-3.17777........

9x = 28.6

x = 28.6/9

Now, we multiply both the numerator and denominator by 10.

x = 286/90

x = 143/45

Therefore the fractional form of the given decimal is 143/45.

(v)  17.215 (bar is for 1 and 5)

Solution:

Let x =  17.2151515...........  -----(1)

As there is the sign bar for two digits, so we have to multiply (1) by 100 on both sides.

100x  =  1721.51515...........------(2)

(2) - (1)  

100x - x  =  1721.51515.......... - 17.2151515...........

99x  =  1704.3

x  =  1704.3/99

Now, we need to multiply both numerator and denominator by 10.

x  =  17043/990

x  =  5681/330

Therefore, the fractional form of the given decimal is 5681/330.

(vi)  -21.2137 (bar is for 7)

Solution:

Let x  =  21.213777...........  -----(1)

As there is the sign bar for two digits, so we have to multiply (1) by 100 on both sides.

10x =  212.137777...........------(2)

(2) - (1)  

10x - x  =  212.137777........... - 21.213777...........

9x  =  191.92

x  =  191.924/9

x  =  190924/9000

x  =  47731/2250

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 10 Chapter Real Numbers