A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
q4πε0a2
zero
3q4πε0a2
4q4πε0a2
The correct Answer is:2

At centre electric field is zero , because facing charges produce equal and opposite electric field.
Topper's Solved these Questions
Similar Questions
A wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionA charge Q is distribution over a metal sphere of radius R. What is the electric field and electric potential at the centre ?
View Solution
Knowledge Check
- Question 1 - Select One
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
 A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj - Question 2 - Select One
A charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
Aλ2πa2ε0Bλ4π2ε0aCλ2πε0aDzero - Question 3 - Select One
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
A closed circuit is in the form of a regular hexagon of side r. If the circuit carries current I, what is the magnetic field induction at the centre of the hexagon?
View SolutionFigures below show regular hexagons, with charges at the vertices. In which of the following cases the electric field at the centre is not zero
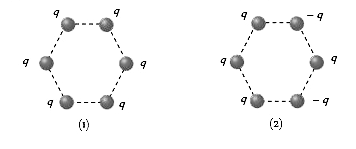
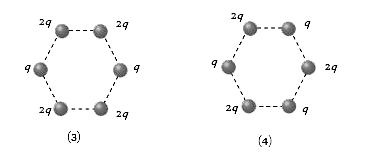 View Solution
View SolutionA hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
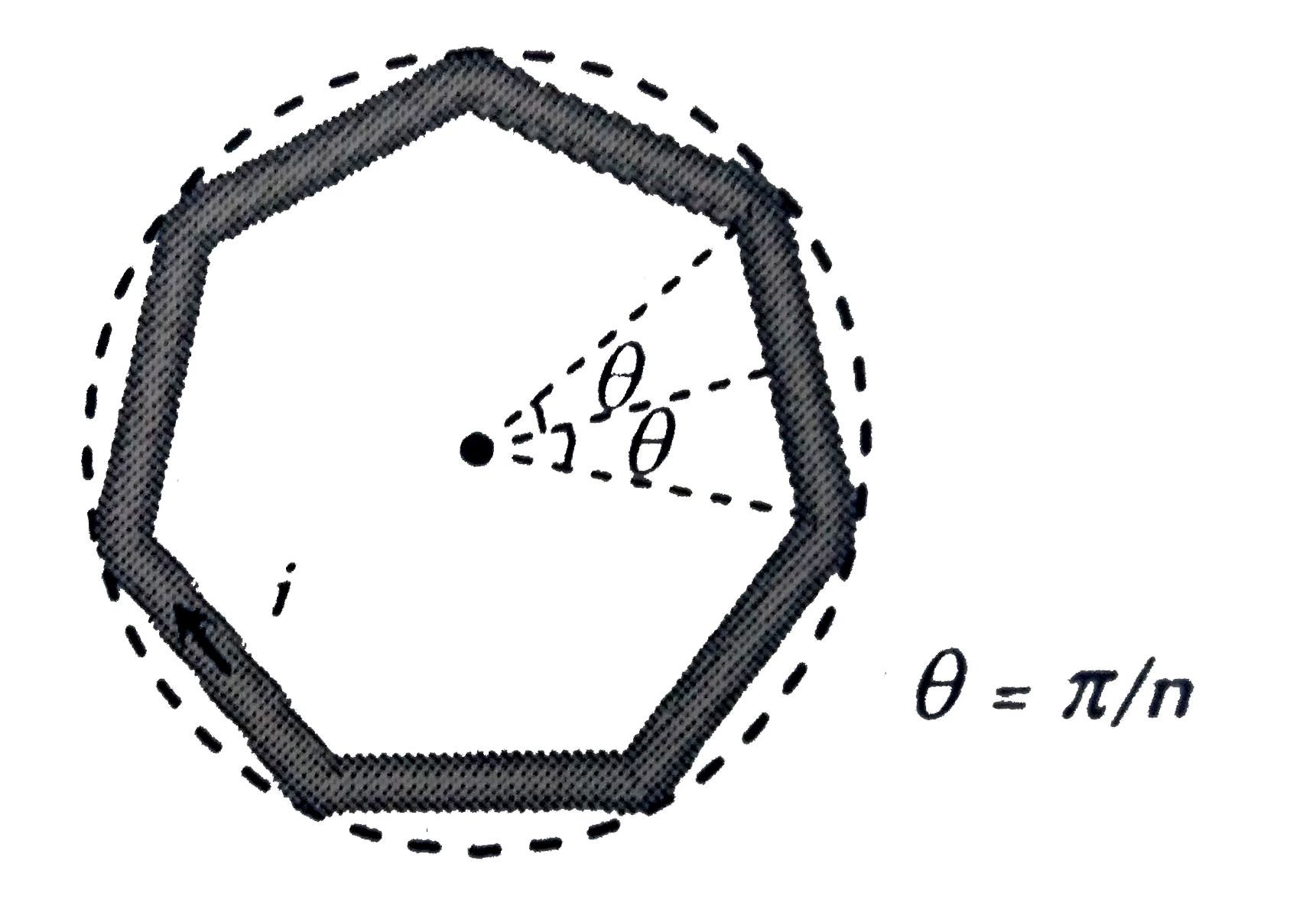 View Solution
View SolutionA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
View Solution

