A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
kq2x(a2+x2)32
2kq2x(a2+x2)32
kq2x(a2+x2)32
kq22x(a2+x2)32
The correct Answer is:C
To find the electric field at a point on the axis of a uniformly charged ring, we can follow these steps:
Step 1: Understand the Geometry
Consider a ring of radius a with a total charge q uniformly distributed along its circumference. We want to find the electric field at a point located on the axis of the ring at a distance x from the center of the ring.
Step 2: Define Charge Element
Let’s consider a small charge element dq on the ring. The total charge q is uniformly distributed, so we can express dq in terms of the linear charge density λ:
λ=q2πa
Thus, for a small arc length ds on the ring, we have:
dq=λds=q2πads
Step 3: Electric Field Due to Charge Element
The electric field dE due to the charge element dq at the point on the axis can be expressed in terms of its components. The electric field dE has two components: one along the axis (let’s call it dEx) and one perpendicular to the axis (let’s call it dEy). Due to symmetry, the dEy components from opposite sides of the ring will cancel out, leaving only the dEx component.
The distance from the charge element to the point on the axis is:
r=√x2+a2
The dE due to dq is given by Coulomb's law:
dE=kdqr2
where k is Coulomb's constant.
Step 4: Resolve Electric Field Components
The component of the electric field along the axis dEx is:
dEx=dE⋅cos(θ)
where cos(θ)=x√x2+a2. Therefore,
dEx=kdqr2⋅x√x2+a2=kdq⋅x(x2+a2)3/2
Step 5: Integrate Over the Ring
Now we need to integrate dEx over the entire ring. The total electric field E at the point on the axis is:
E=∫dEx=∫kdq⋅x(x2+a2)3/2
Since dq=q2πads and ds=adθ (where θ is the angle parameterizing the ring), we have:
dq=q2πdθ
Thus,
E=∫2π0k⋅q2π⋅x(x2+a2)3/2dθ
The integral simplifies to:
E=k⋅q⋅x(x2+a2)3/2⋅∫2π012πdθ=k⋅q⋅x(x2+a2)3/2
Step 6: Final Expression
Thus, the electric field at a distance x from the center of the ring along the axis is:
E=k⋅q⋅x(x2+a2)3/2
Consider a ring of radius a with a total charge q uniformly distributed along its circumference. We want to find the electric field at a point located on the axis of the ring at a distance x from the center of the ring.
Let’s consider a small charge element dq on the ring. The total charge q is uniformly distributed, so we can express dq in terms of the linear charge density λ:
λ=q2πa
Thus, for a small arc length ds on the ring, we have:
dq=λds=q2πads
The electric field dE due to the charge element dq at the point on the axis can be expressed in terms of its components. The electric field dE has two components: one along the axis (let’s call it dEx) and one perpendicular to the axis (let’s call it dEy). Due to symmetry, the dEy components from opposite sides of the ring will cancel out, leaving only the dEx component.
r=√x2+a2
dE=kdqr2
where k is Coulomb's constant.
The component of the electric field along the axis dEx is:
dEx=dE⋅cos(θ)
where cos(θ)=x√x2+a2. Therefore,
dEx=kdqr2⋅x√x2+a2=kdq⋅x(x2+a2)3/2
Now we need to integrate dEx over the entire ring. The total electric field E at the point on the axis is:
E=∫dEx=∫kdq⋅x(x2+a2)3/2
Since dq=q2πads and ds=adθ (where θ is the angle parameterizing the ring), we have:
dq=q2πdθ
Thus,
E=∫2π0k⋅q2π⋅x(x2+a2)3/2dθ
The integral simplifies to:
E=k⋅q⋅x(x2+a2)3/2⋅∫2π012πdθ=k⋅q⋅x(x2+a2)3/2
Thus, the electric field at a distance x from the center of the ring along the axis is:
E=k⋅q⋅x(x2+a2)3/2
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Worked Out Examples
19 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Short Answer
14 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Mass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionA thin circular ring of radius r is uniformly charged over its length.Consider two points,the centre of ring 0 ,and a point P on the axis of the ring at a distance a from the centre of the ring.If ratio of potential at points O and P is V0Vp=√101, then value of ar is ..
View Solution
Knowledge Check
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
 A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A thin circular ring of radius r is uniformly charged over its length.Consider two points the centre of ring 0 and a point P on the axis of the ring at a distance a from the centre of the ring.If ratio of potential at points 0 and P is (V_(0))/(V_(p))=(sqrt(10))/(1) then value of (a)/(r) is
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA ring of radius r has a uniformly spread charge + q on quarter of its circumference. The opposite quarter of the ring carries a charge – q uniformly spread over it. Find the electric potential at a point A shown in the figure. Point A is at a distance R(gtgt r) from the centre of the ring.
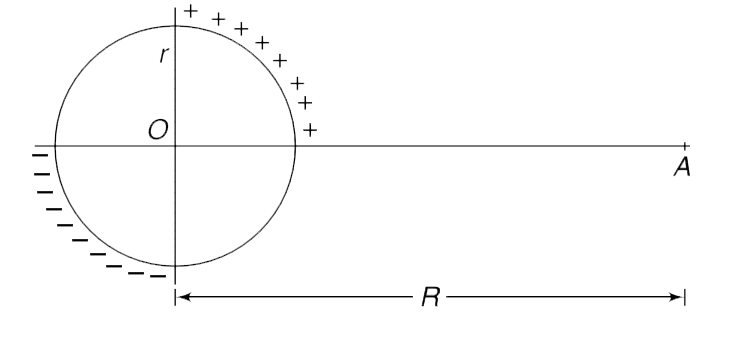
View SolutionConsider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View SolutionConsider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View Solution
