A wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
qε0l2
q2(ε0l2)
q4π(ε0l2)
q2π(ε0l2)
To find the electric field at the center of a semicircular wire of length l and charge q uniformly distributed along its length, we can follow these steps:
Step 1: Define the charge density
The linear charge density λ is defined as the total charge q divided by the length l of the wire:
λ=ql
Step 2: Consider a small charge element
Consider a small element of the wire dθ at an angle θ from the vertical. The length of this small element ds on the semicircle is given by:
ds=rdθ
where r is the radius of the semicircle.
The charge dq on this small element is:
dq=λds=λrdθ=ql⋅rdθ
Step 3: Calculate the electric field due to dq
The electric field dE at the center of the semicircle due to the charge dq is directed radially inward. The magnitude of this electric field is given by Coulomb's law:
dE=kdqr2=kdqr2=kλrdθr2=kλdθr
where k is Coulomb's constant (k=14πϵ0).
Step 4: Resolve the electric field into components
The electric field dE can be resolved into two components: a vertical component dEy and a horizontal component dEx. Due to symmetry, the horizontal components from opposite sides will cancel out, and we only need to consider the vertical components:
dEy=dEsin(θ)=kλrdθsin(θ)
Step 5: Integrate to find the total electric field
The total vertical electric field Ey at the center is obtained by integrating dEy from θ=0 to θ=π:
Ey=∫π0dEy=∫π0kλrsin(θ)dθ
Step 6: Evaluate the integral
The integral of sin(θ) from 0 to π is:
∫π0sin(θ)dθ=2
Thus, we have:
Ey=kλr⋅2=2kλr
Step 7: Substitute λ and r
Substituting λ=ql and r=lπ (since the length of the semicircle is πr=l):
Ey=2kqllπ=2kqπl2
Step 8: Substitute k
Substituting k=14πϵ0:
Ey=2⋅14πϵ0⋅qπl2=q2ϵ0l2
Final Answer
Thus, the electric field at the center of the semicircle is:
E=q2ϵ0l2
---
The linear charge density λ is defined as the total charge q divided by the length l of the wire:
λ=ql
Consider a small element of the wire dθ at an angle θ from the vertical. The length of this small element ds on the semicircle is given by:
ds=rdθ
where r is the radius of the semicircle.
dq=λds=λrdθ=ql⋅rdθ
The electric field dE at the center of the semicircle due to the charge dq is directed radially inward. The magnitude of this electric field is given by Coulomb's law:
dE=kdqr2=kdqr2=kλrdθr2=kλdθr
where k is Coulomb's constant (k=14πϵ0).
The electric field dE can be resolved into two components: a vertical component dEy and a horizontal component dEx. Due to symmetry, the horizontal components from opposite sides will cancel out, and we only need to consider the vertical components:
dEy=dEsin(θ)=kλrdθsin(θ)
The total vertical electric field Ey at the center is obtained by integrating dEy from θ=0 to θ=π:
Ey=∫π0dEy=∫π0kλrsin(θ)dθ
The integral of sin(θ) from 0 to π is:
∫π0sin(θ)dθ=2
Thus, we have:
Ey=kλr⋅2=2kλr
Substituting λ=ql and r=lπ (since the length of the semicircle is πr=l):
Ey=2kqllπ=2kqπl2
Substituting k=14πϵ0:
Ey=2⋅14πϵ0⋅qπl2=q2ϵ0l2
Thus, the electric field at the center of the semicircle is:
E=q2ϵ0l2
Topper's Solved these Questions
Similar Questions
A wire of length 36 cm is bent in the form of a semicircle. What is the radius of the semicircle?
View SolutionA positive charge Q is uniformly distributed across a rod of length L. The rod is then bent in the form of a semicircle. What will be the electric field intensity at the centre of curvature of the semicircle thus formed?
View Solution
Knowledge Check
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2A wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
 AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axis
AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axissemicircle of radius R. The electric field at the centre is -
A2kλRBkλ2RCZeroDNone
Positive charge Q is uniformly distributed across a thin rod of length L. The rod is then bent in the form of a semicircle. What will be the electric potential at the centre of curvature of semicircle formed?
View SolutionFigure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
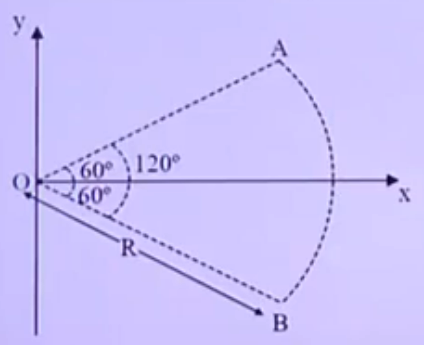
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

View SolutionA charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
View SolutionAn iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
View Solution
