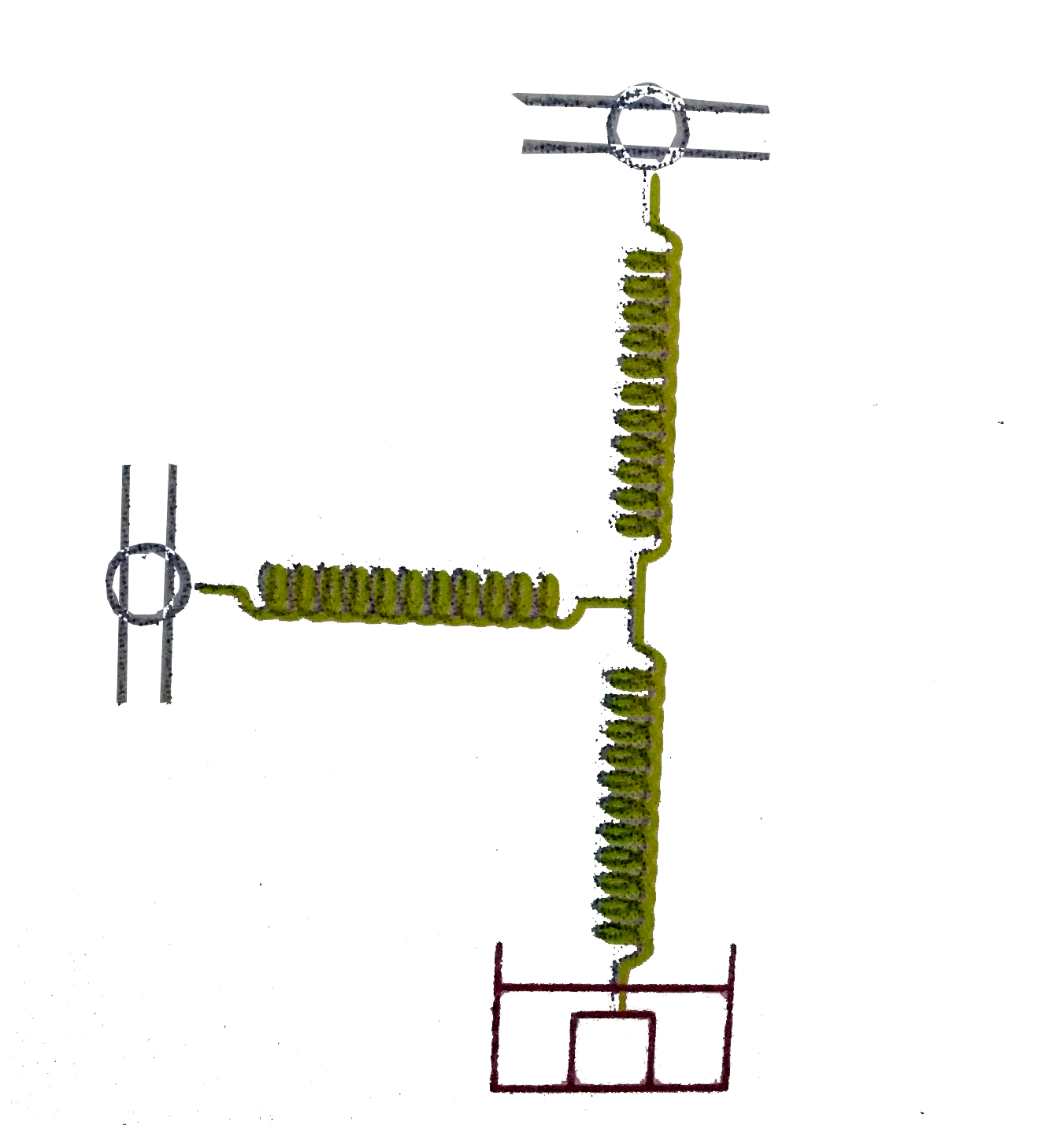
Three springs A,B and C each of force constant K, are connected at O. The other ends of B and C can slide on smooth sliders. A pan is hanging from other end of the spring A. When a block of mass m is placed into he pan, find the amount of workdone by the gravity on block system after it stops vibrating. The spring C does not sag :
 .
.
3m2g22K
m2g2K
2m2g2K
m2g22K
The correct Answer is:C
The system will adjust in such a way by sliding the spring C remains instretched and spring A and B remains vertical. Thus, effective force constant is given by
1K'=1K+1K,K'=K2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Multiple Answer)11videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Comprehension)20videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Integer)5videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
- Question 1 - Select One
A spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv) - Question 2 - Select One
In the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
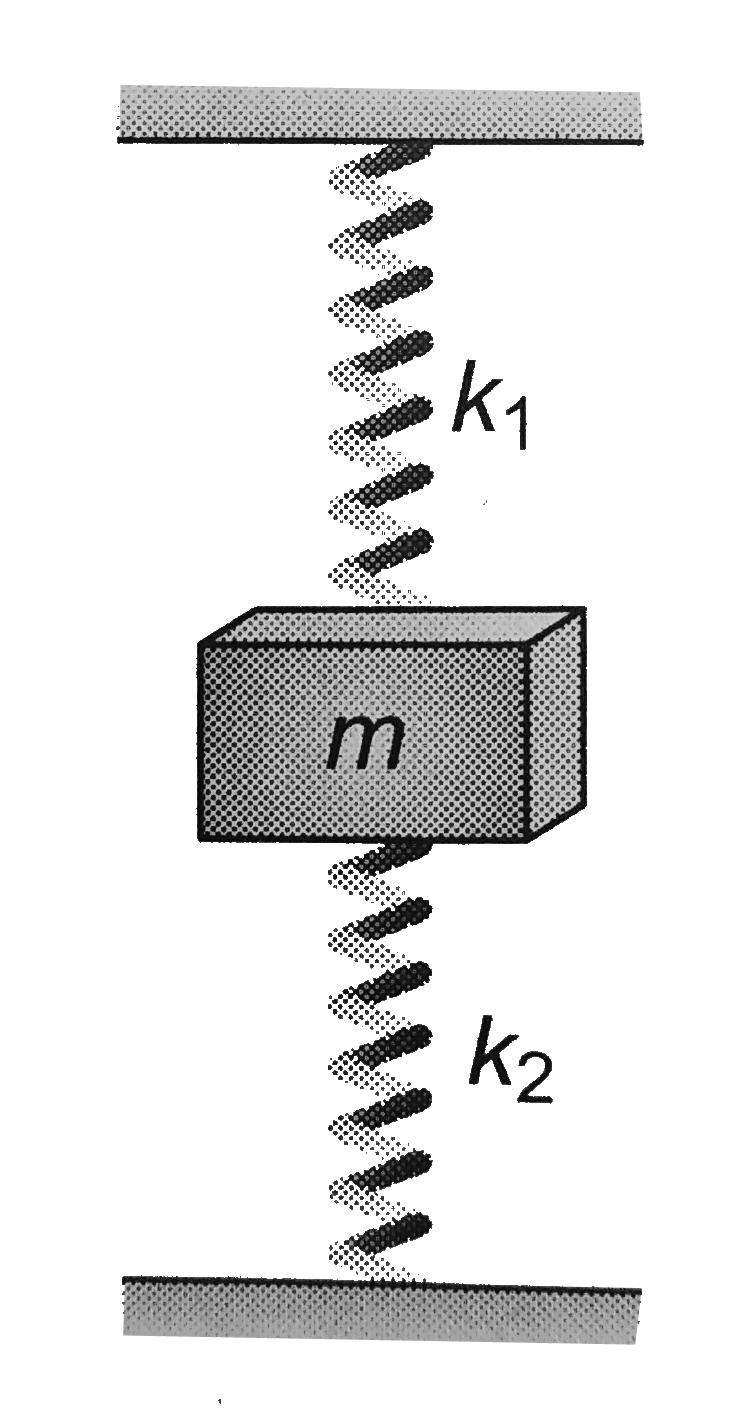 Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated. - Question 3 - Select One
An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2k
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
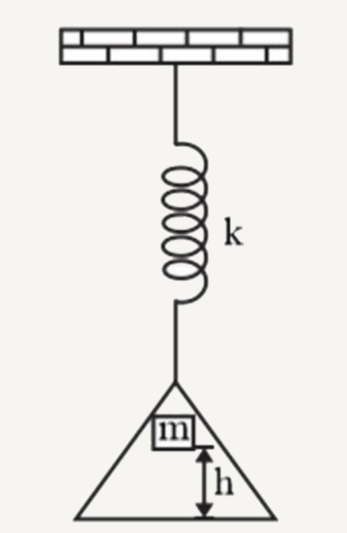 View Solution
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 View Solution
View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 View Solution
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
 View Solution
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution

