The work done an a particle of mass m by a force
K⎡⎢
⎢⎣x(x2+y2)3/2ˆi+y(x2+y23/2)ˆj⎤⎥
⎥⎦<br>(Kbe∈gaconstantofap∝riatedimensions),whentheparticalistakenomthep∮(a,0)→thep∮(0,a) along a circular path of radius a about the origin in x - y plane is
A
2kπa
B
kπa
C
kπ2a
D
zero
Video Solution
Text Solution
The correct Answer is:D
W=∫→F.d→r
=krB∫rA[xˆi(x2+y2)3/2+yˆj(x2+y2)3/2](dxˆi+dyˆj)
=krB∫rAxdx(x2+y2)+ydy(x2+y2)3/2
=krB∫rA1(x2+y2)3/2[d(x22)+d(y22)]
=krB∫rA1(x2+y2)3/2(x2+y2)
=krB∫rA12r3d(r2)=krB∫rA2rdr2r3=krB∫rAdrr2
=k[−1r]rBrA=k[1rA−1rB]
But rA=aand rB=a , ∴W=0.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Multiple Answer)11videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Comprehension)20videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Integer)5videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum distance of the point (a, 0) from the curve 2x2+y2−2x=0 is -
A√1+2k−k2B√1−2k+2k2C√1+2k+2k2D√1−2k+k2 - Question 2 - Select One
A force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
A−2Ka2B2Ka2C−Ka2DKa2 - Question 3 - Select One
A force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
A−2Ka2B2Ka2C−Ka2DKa2
If the image of the point (1,2,3) in the plane x+2y=0 is (h,k,l)then l=
View SolutionThe maximum distance of the point (k,0) from the curve 2x2+y2−2x=0 is equal to
View SolutionThe distance of a point (2,3) from the line 2x -3y + 9 = 0 measured along a line x-y +1 =0 is :
View SolutionLocus of image of the point (2,3) in the line (2x−3y+4)+k(x−2y+3)=0,k in R is
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
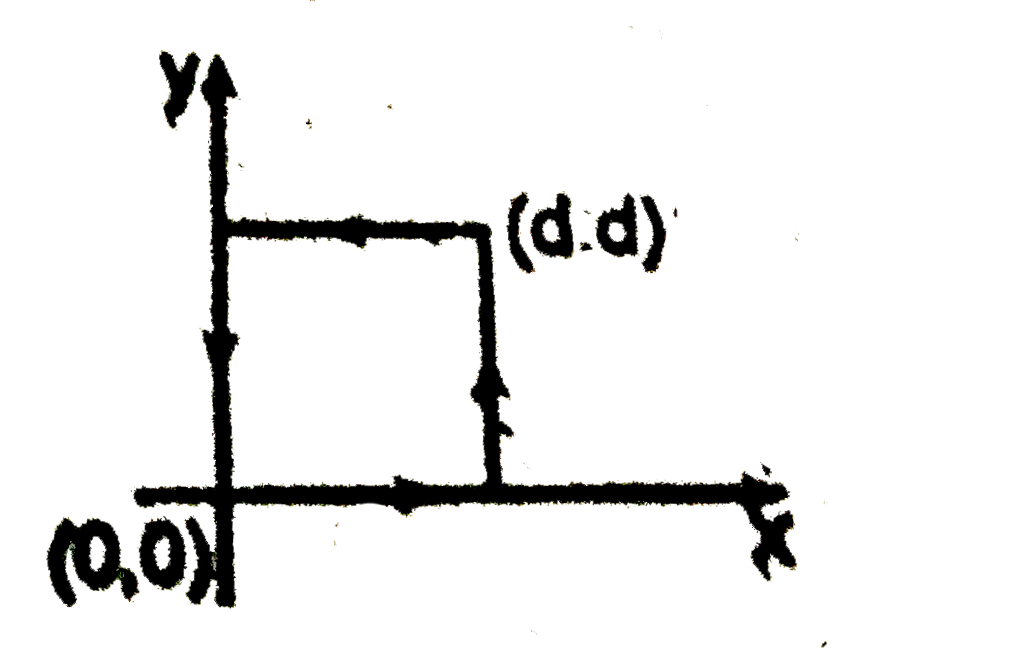 View Solution
View Solution

