A small body A starts sliding from the height h down an inclined groove passing into a half-circle of radius h/2 (figure).
Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).
√927gh
√827gh
√278gh
√1027gh
The correct Answer is:B
v2 (at end of track) =2gh
Let body break at angle θ the mu2h2=mgcosθ…(1)
u2=v2−2gh2(1+cosθ)
solving cosθ=23 & u=√23gh
v at highest Pt is
ucosθ=√23gh×23=√827gh.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Multiple Answer)11videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Comprehension)20videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Integer)5videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
A small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
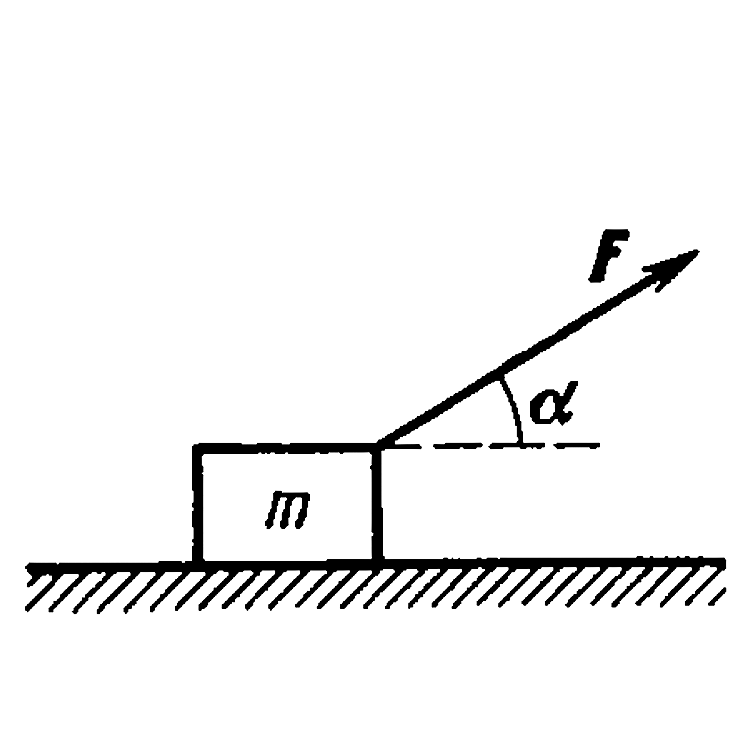View Solution
Knowledge Check
- Question 1 - Select One
A body A is dropped from a height h above the ground. At the same time another body B (at a horizontal' distance d from the line of fall of A) is fired from the ground at an angle α to the horizontal. If the two bodies collide at the highest point of the trajectory of B the angle of projection is given by
Aα=tan−1(dh)Bα=sin−1(hd)Cα=tan−1(hd)Dα=cos−1(hd) - Question 2 - Select One
A body of mass m is released from a height h on a smooth inclined plane that is shown in the figure. The following can be true about the velocity of the block knowing that the wedge is fixed.
.Av is highest when it just touches the springBv is highest when it compresses the spring by some amountCv is highest when the spring comes back to natural positionDv is highest at the maximum compression - Question 3 - Select One
A body slides down a fixed curved track that is one quadrant of a circle of radius R, as in the figure. If there is no friction and the body starts from rest, its speed at the bottom of the track is
A5gRB√5gRC√2gRD√gR
A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
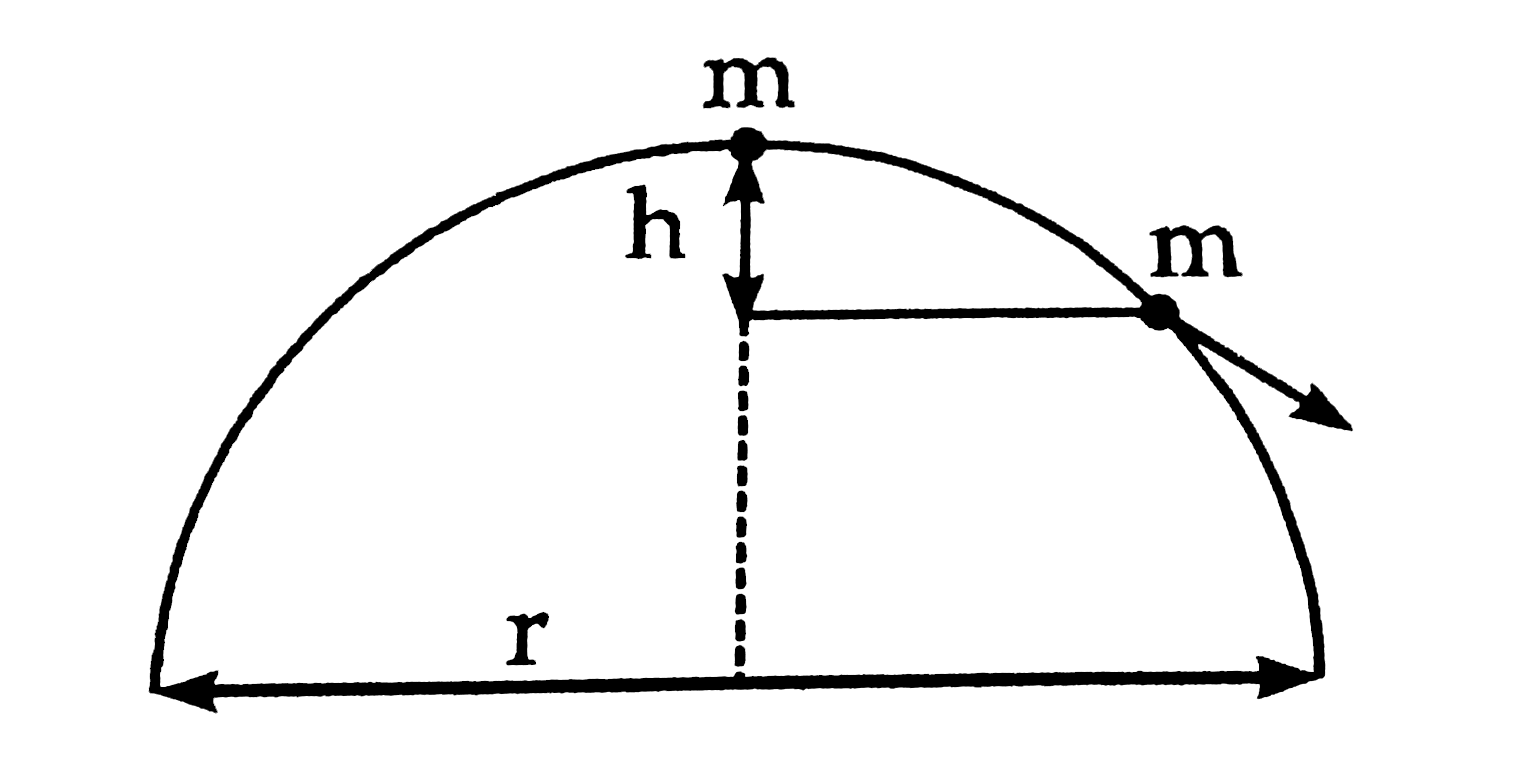View SolutionA body is thrown from the surface of the Earth at an angle α to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the time of motion,
(b) the maximum height of ascent and the horizontal range, at what value of the angle α they will be equal to each other,
(c) the equation of trajectory y(x), where y and x are displacements of the body along the vertical and the horizontal respectively,
(d) the curvature radii of trajectory at its initial point and at its peak.View SolutionIn the system shown in figure the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body m1 and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t=0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.
View SolutionA small sphereical ball is released from a point at a height h on a rough track shown in figure. Assuming that it dow not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
View SolutionAt the equator a stationary (relative to the Earth) body falls down from the height h=500m. Assuming the air drag to be negligible, find how much off the vertical, and in what direction, the body will deviate when it hits the ground.
View Solution