A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
2√2+1
1√2+1
2√2−1
1√2−1
The correct Answer is:A
Let the stone is projected with a velocity u at an angle θ with the horizontal, we have
(2h)=(usinθ)22gorusinθ=2√gh
Suppose t is the time taken by the stone to reach the height h above the ground.Then
h=usinθt−12gt2orgt22−usinθt+h=0
As we have usinθ=2√gh
∴(gt)22−2√ght+h=0
Solving above equation for t, we get
t=2√gh±√(2√gh)2−4×ghh2×g2&t2√2hg(√2+1)
Where t1 and t2 correspond to P and Q in the figure.Suppose v is the horizontal velocity of the bird. Then PQ=vt2.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer
16 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-VI Passage answer
18 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer
6 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
A stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10ms−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
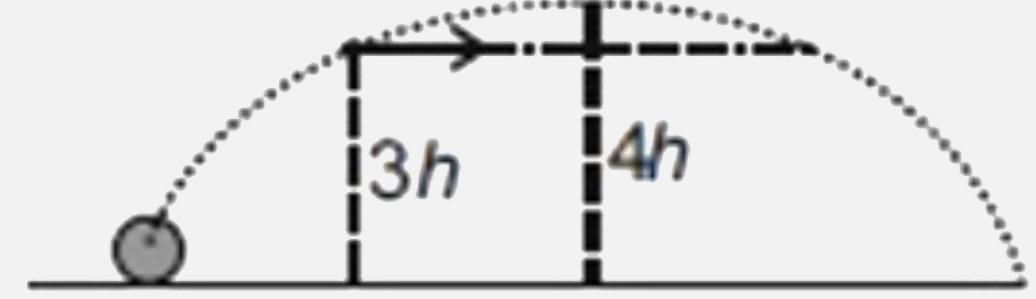
View SolutionA stone is projected at an angle α to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot α from the foot of the lower.
View Solution
Knowledge Check
Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5A stone is projected at an angle α to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
A6htanαB6hcotαChtanαDhcotαIf T be the total time of flight and H be the maximum height attained by a stone from the point of projection, then H/T will be ( u=projection velocity and θ=projection angle )
A(1/2)sinθB(1/4)usinθCusinθD2u sinθ
If the horizontal range of a projectile be a and the maximum height attained by it is b, then prove that the velocity of projection is
View SolutionA body is projected vertically up from ground with a velocity u so as to reach maximum height 'h'. At half of the maximum height its velocity will be
View SolutionA body is projected horizontally from the top of a tower with initial velocity 18ms−1. It hits the ground at angle 45∘. What is the vertical component of velocity when it strikes the ground ?
View SolutionA body is thrown horizontally from the top of a tower. It reaches the ground after 4s at an angle 45∘ to the ground. The velocity of projection is
View SolutionA body of mass m is projected from ground with speed u at an angle θ with horizontal. The power delivered by gravity to it at half of maximum height from ground is
View Solution
