Compute the area bounded by the lines x+2y=2;y−x=1 and 2x+y=7
To find the area bounded by the lines x+2y=2, y−x=1, and 2x+y=7, we will follow these steps:
Step 1: Find the intersection points of the lines.
1. Intersection of Line 1 and Line 2:
- Line 1: x+2y=2
- Line 2: y−x=1⇒y=x+1
- Substitute y from Line 2 into Line 1:
x+2(x+1)=2⟹x+2x+2=2⟹3x+2=2⟹3x=0⟹x=0
- Substitute x=0 back into Line 2:
y=0+1=1
- Intersection point: (0,1)
2. Intersection of Line 2 and Line 3:
- Line 3: 2x+y=7
- Substitute y from Line 2 into Line 3:
2x+(x+1)=7⟹3x+1=7⟹3x=6⟹x=2
- Substitute x=2 back into Line 2:
y=2+1=3
- Intersection point: (2,3)
3. Intersection of Line 1 and Line 3:
- Substitute y from Line 1 into Line 3:
2x+(2−x)=7⟹2x+2−x=7⟹x+2=7⟹x=5
- Substitute x=5 back into Line 1:
5+2y=2⟹2y=2−5⟹2y=−3⟹y=−32
- Intersection point: (5,−32)
Step 2: Identify the area bounded by the lines.
The intersection points we found are:
1. A(0,1)
2. B(2,3)
3. C(5,−32)
Step 3: Set up the integrals to find the area.
1. Determine the area between the curves.
- From x=0 to x=2, the upper curve is Line 2 and the lower curve is Line 1.
- From x=2 to x=5, the upper curve is Line 3 and the lower curve is Line 1.
2. Calculate the area:
- Area A can be expressed as:
A=∫20((x+1)−(1−x2))dx+∫52(7−2x−(1−x2))dx
Step 4: Evaluate the integrals.
1. First integral:
∫20((x+1)−(1−x2))dx=∫20(x+1−1+x2)dx=∫20(3x2)dx
=32⋅x22∣∣∣20=32⋅42=3
2. Second integral:
∫52(7−2x−(1−x2))dx=∫52(6−3x2)dx
=(6x−3x24)∣∣∣52=(30−754)−(12−3)=(30−18.75)−9=1.25
Final Area Calculation:
A=3+1.25=4.25
Conclusion:
The area bounded by the lines x+2y=2, y−x=1, and 2x+y=7 is 4.25 square units.
- Line 1: x+2y=2
- Line 2: y−x=1⇒y=x+1
- Substitute y from Line 2 into Line 1:
x+2(x+1)=2⟹x+2x+2=2⟹3x+2=2⟹3x=0⟹x=0
- Substitute x=0 back into Line 2:
y=0+1=1
- Intersection point: (0,1)
- Line 3: 2x+y=7
- Substitute y from Line 2 into Line 3:
2x+(x+1)=7⟹3x+1=7⟹3x=6⟹x=2
- Substitute x=2 back into Line 2:
y=2+1=3
- Intersection point: (2,3)
- Substitute y from Line 1 into Line 3:
2x+(2−x)=7⟹2x+2−x=7⟹x+2=7⟹x=5
- Substitute x=5 back into Line 1:
5+2y=2⟹2y=2−5⟹2y=−3⟹y=−32
- Intersection point: (5,−32)
1. A(0,1)
2. B(2,3)
3. C(5,−32)
- From x=0 to x=2, the upper curve is Line 2 and the lower curve is Line 1.
- From x=2 to x=5, the upper curve is Line 3 and the lower curve is Line 1.
- Area A can be expressed as:
A=∫20((x+1)−(1−x2))dx+∫52(7−2x−(1−x2))dx
∫20((x+1)−(1−x2))dx=∫20(x+1−1+x2)dx=∫20(3x2)dx
=32⋅x22∣∣∣20=32⋅42=3
∫52(7−2x−(1−x2))dx=∫52(6−3x2)dx
=(6x−3x24)∣∣∣52=(30−754)−(12−3)=(30−18.75)−9=1.25
A=3+1.25=4.25
The area bounded by the lines x+2y=2, y−x=1, and 2x+y=7 is 4.25 square units.
Similar Questions
Knowledge Check
Area bounded by the lines x=2y,y=2x and x = 4 is
A14B13C10D12Area bounded by the lines y=2x,y=4x and x = 2 is
A8B4C5DNone of theseThe area bounded by the curves y=x2andy=2−x2 is
A83 sq unitsB3/8 sq unitsC3/2 sq unitsDNone of these
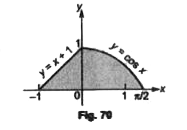
Compute the area of the figure bounded by the lines y=x+1,y=cosx and the x-axis
View SolutionThe area bounded by the lines y=|x−2|,|x|=3 and y=0 is
View SolutionCompute, using integration, the area bounded by the lines Given lines x+2y=2,y−x=1,2x+y=7 is
View SolutionThe area bounded by the curve y=2x−x2 and the line y = - x is
View SolutionThe area bounded by the curves y2=x3and|y|=2x is
View Solution
