Compute the area bounded by the lines x+2y=2,y−x=1 and 2x+y=7.
The correct Answer is:N/a
To find the area bounded by the lines x+2y=2, y−x=1, and 2x+y=7, we will follow these steps:
Step 1: Find the intersection points of the lines
We need to find the points where these lines intersect, as these points will form the vertices of the bounded area.
1. Intersection of x+2y=2 and y−x=1:
- From y−x=1, we can express y in terms of x:
y=x+1
- Substitute y in the first equation:
x+2(x+1)=2⟹x+2x+2=2⟹3x+2=2⟹3x=0⟹x=0
- Substitute x=0 back to find y:
y=0+1=1
- So, the intersection point is (0,1).
2. Intersection of y−x=1 and 2x+y=7:
- Again, using y=x+1:
2x+(x+1)=7⟹2x+x+1=7⟹3x+1=7⟹3x=6⟹x=2
- Substitute x=2 back to find y:
y=2+1=3
- So, the intersection point is (2,3).
3. Intersection of x+2y=2 and 2x+y=7:
- From x+2y=2, express y:
2y=2−x⟹y=1−x2
- Substitute y in the second equation:
2x+(1−x2)=7⟹2x+1−x2=7⟹4x−x2=6⟹3x2=6⟹3x=12⟹x=4
- Substitute x=4 back to find y:
y=1−42=1−2=−1
- So, the intersection point is (4,−1).
Step 2: Identify the vertices of the bounded area
The vertices of the bounded area formed by the intersection points are:
1. A(0,1)
2. B(2,3)
3. C(4,−1)
Step 3: Set up the integral to find the area
The area can be calculated by integrating the difference between the upper and lower functions over the range of x values from 0 to 4.
1. From x=0 to x=2:
- The upper curve is y=1+x (from y−x=1).
- The lower curve is y=1−x2 (from x+2y=2).
- The area A1 is given by:
A1=∫20((1+x)−(1−x2))dx=∫20(1+x−1+x2)dx=∫20(3x2)dx
2. From x=2 to x=4:
- The upper curve is y=7−2x (from 2x+y=7).
- The lower curve is y=1−x2.
- The area A2 is given by:
A2=∫42((7−2x)−(1−x2))dx=∫42(6−3x2)dx
Step 4: Calculate the integrals
1. Calculate A1:
A1=∫203x2dx=32⋅(x22)20=32⋅(222−0)=32⋅2=3
2. Calculate A2:
A2=∫42(6−3x2)dx=(6x−3x24)42
- Evaluating at the limits:
=(6(4)−3(42)4)−(6(2)−3(22)4)
=(24−12)−(12−3)=12−9=3
Step 5: Total Area
The total area A is:
A=A1+A2=3+3=6
Final Answer
The area bounded by the lines x+2y=2, y−x=1, and 2x+y=7 is 6 square units.
We need to find the points where these lines intersect, as these points will form the vertices of the bounded area.
- From y−x=1, we can express y in terms of x:
y=x+1
- Substitute y in the first equation:
x+2(x+1)=2⟹x+2x+2=2⟹3x+2=2⟹3x=0⟹x=0
- Substitute x=0 back to find y:
y=0+1=1
- So, the intersection point is (0,1).
- Again, using y=x+1:
2x+(x+1)=7⟹2x+x+1=7⟹3x+1=7⟹3x=6⟹x=2
- Substitute x=2 back to find y:
y=2+1=3
- So, the intersection point is (2,3).
- From x+2y=2, express y:
2y=2−x⟹y=1−x2
- Substitute y in the second equation:
2x+(1−x2)=7⟹2x+1−x2=7⟹4x−x2=6⟹3x2=6⟹3x=12⟹x=4
- Substitute x=4 back to find y:
y=1−42=1−2=−1
- So, the intersection point is (4,−1).
The vertices of the bounded area formed by the intersection points are:
1. A(0,1)
2. B(2,3)
3. C(4,−1)
The area can be calculated by integrating the difference between the upper and lower functions over the range of x values from 0 to 4.
- The upper curve is y=1+x (from y−x=1).
- The lower curve is y=1−x2 (from x+2y=2).
- The area A1 is given by:
A1=∫20((1+x)−(1−x2))dx=∫20(1+x−1+x2)dx=∫20(3x2)dx
- The upper curve is y=7−2x (from 2x+y=7).
- The lower curve is y=1−x2.
- The area A2 is given by:
A2=∫42((7−2x)−(1−x2))dx=∫42(6−3x2)dx
1. Calculate A1:
A1=∫203x2dx=32⋅(x22)20=32⋅(222−0)=32⋅2=3
A2=∫42(6−3x2)dx=(6x−3x24)42
- Evaluating at the limits:
=(6(4)−3(42)4)−(6(2)−3(22)4)
=(24−12)−(12−3)=12−9=3
The total area A is:
A=A1+A2=3+3=6
The area bounded by the lines x+2y=2, y−x=1, and 2x+y=7 is 6 square units.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Area bounded by the lines y=2x,y=4x and x = 2 is
A8B4C5DNone of these - Question 2 - Select One
Area bounded by the lines x=2y,y=2x and x = 4 is
A14B13C10D12 - Question 3 - Select One
The area of the reggion bounded by the lines y=2x+1,y=3x+1 and x=4 is
A16 sq. unitsB1213 sq. unitsC1216 sq. unitsD8 sq. units
Compute, using integration, the area bounded by the lines Given lines x+2y=2,y−x=1,2x+y=7 is
View SolutionThe area bounded by the lines y=||x−1|−2| and x axis is
View SolutionCompute the area of the figure bounded by the lines y=x+1,y=cosx and the x-axis
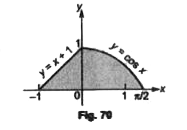 View Solution
View SolutionThe area bounded by the curves y=x2andy=2−x2 is
View SolutionThe area bounded by the curves y2=x3and|y|=2x is
View Solution

