Number of A parabola of the form y=ax2+bx+c with a>0 intersection (s)of these graph of f(x)=1x2−4 .number of a possible distinct intersection(s) of these graph is
0
2
3
4
The correct Answer is:B, C, D
Step by step video, text & image solution for Number of A parabola of the form y= ax^2 +bx+c with a>0 intersection (s)of these graph of f(x)=1/(x^2-4) .number of a possible distinct intersection(s) of these graph is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)16videos
APPLICATION OF DERIVATIVES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (MATHCING TYPE PROBLEMS)1videos
APPLICATION OF DERIVATIVES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)22videos
APPLICATION OF DERIVATIVES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (SUBJECTIVE TYPE PROBLEMS)8videos
AREA UNDER CURVES
Similar Questions
Graphical representation of different functions is also a method of find the number of solution (s) of any equation. The number of solution of the equation f1(x)=f2(x) is equal to the number of points of intersection of the graphs of y=f1(c)andy=f2(x). Now consider the equation
|x−1+|x−2|+|x−3∣=k. If k>2, then the number of solutions of the given equation is/areView SolutionDraw the graph of the linear equation y-x=2. Find the points of intersection of it with both axes.
View Solution
Knowledge Check
- Question 1 - Select One
Statement-1: Number of solutions of the equation cos(x−1)=|x−1|10 are 6.
Statement -2: Number of solutions of the equation f(x) = g(x) is equal to the number of points of intersection of graph y = f(x) and y = g(x)AStatement -1 is true, statement -2 is True and Statement -2 is a correct explanation for statement -1.BStatement -1 is true, statement -2 is True and Statement -2 is NOT a correct explanation for statement -1.CStatement -1 is True , Statement -2 is FalseDStatement -1 is False, Statement -2 is True - Question 2 - Select One
The graphs of x=aandy=b intersect at
A(a,b)B(b,a)C(-a,b)D(a,-b) - Question 3 - Select One
What will be the number of the zero (s), if the graph of a quadratic polynomial does not intersect the x-axis ?
AzeroBoneCtwoDthree
If a>0 and b2−4ac<0, then the graph of y=ax2+bx+c
View SolutionIf fig shows the graph of f(x)=ax2+bx+c,then Fig ac<0 b. bc>0 c. ab>0 d. abc<0
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, find the sign of a,bandc.
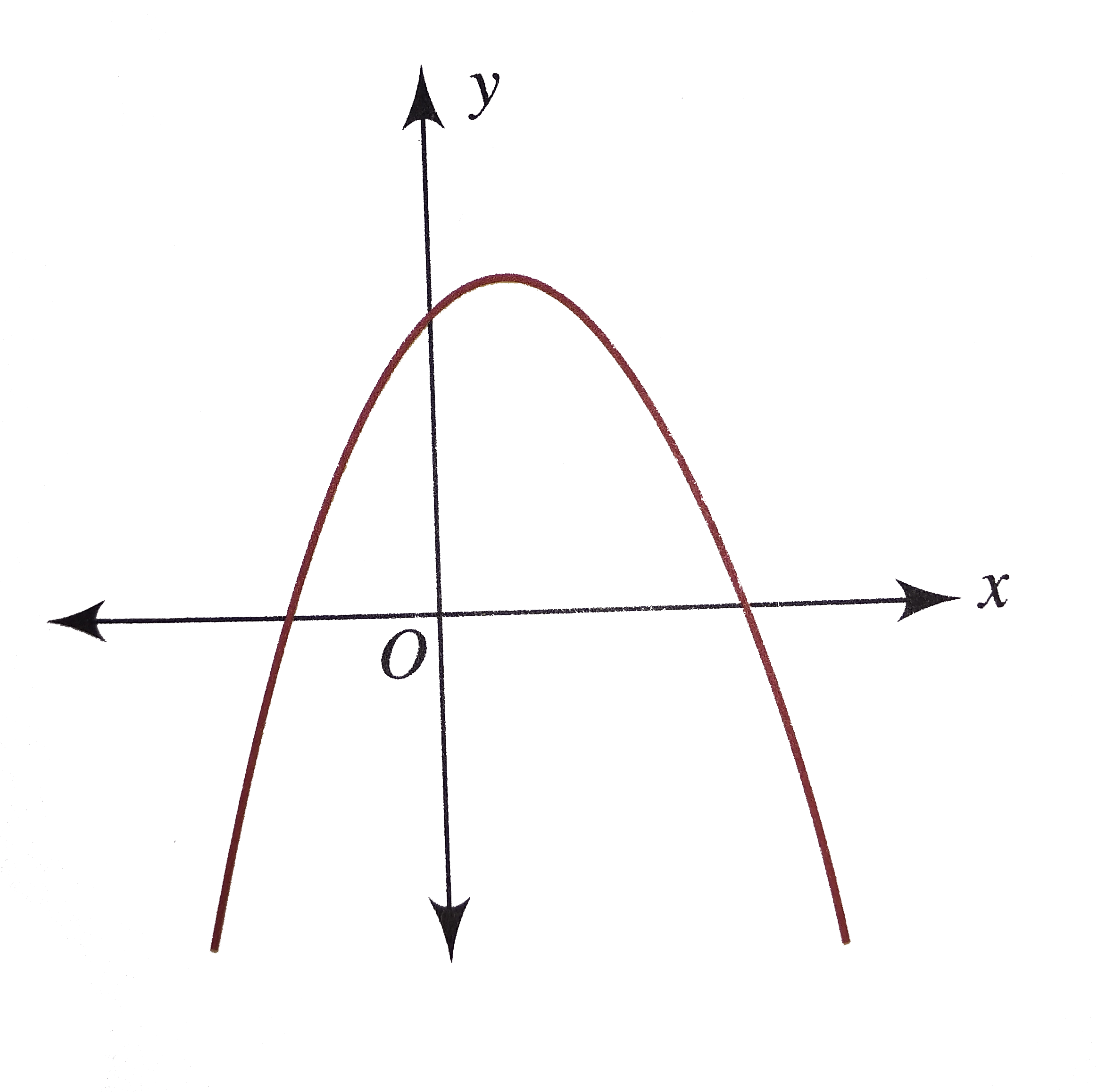 View Solution
View SolutionNumber of points in which the graphs of |y|=x+1 and (x-1)^(2)+y^(2)=4 intersect,is (A) 1
View SolutionThe graphs of the polynomial x2−1 and cos x intersect
View Solution

