Two sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
same as that B
opposite to that of B
θ=tan−1(1/2) to the x-axis
θ=tan−1(−1/2) to the x-axis
The correct Answer is:D
Momentum conservation :
x:m2v=m1cosθ(i)⇒vcosθ=m2m1v
y:0=m2v2−m1vsinθ(ii)⇒vsinθ=m2m1v2
tanthet=vsinθvcosθ=12⇒θ=tan−1(12)
SInce A is moving below the x-axis , hence the angle will be tan−1(−12) to the axis.
Note : A angles measured in the anticlockwise direction are considered +ve and in clockwise , −ve.

Topper's Solved these Questions
Similar Questions
Two balls A and B of masses 0.3 kg and 0.2 kg respectively are moving along positive X-axis and negaive X-axis with velocities 2.0 m / s. They collide and thereafter move in the directions opposite to their original directions. Find the velocities of A and B after collision. Also, calculate total K.E. of the ball before and after collision.
View SolutionA ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View Solution
Knowledge Check
- Question 1 - Select One
Two spheres a and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the x-axisDθ=tan−1(−12) to the x-axis - Question 2 - Select One
Two spheres A and B of masses m1andm2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v2direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the axisDθ=tan−1(−12) to the x-axis - Question 3 - Select One
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
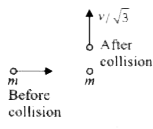 View Solution
View SolutionA body of mass m moving at a constant velocity v hits another body of the same mass moving with a velocity v/2 but in the opposite direction and sticks to it. The common velocity after collision is
View Solution

