Two trolleys of mass m and 3 m are attached by a spring. The spring wa

Topper's Solved these Questions

BOOK - CP SINGHCHAPTER - CENTER OF MASSEXERCISE - Exercises
150videos
CENTER OF MASS
BOOK - CP SINGHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise
90videos
CIRCULAR MOTION

Knowledge Check

Question 1 - Select One
Two trolleys of masses m and 3m are connected by a spring. They are compressed and released, they move off in opposite direction and come to rest after covering distances $s_{1} and s_{2}$ respectively. If the frictional force between trolley and surface is same in both the cases then the ratio of distances $s_{1} : s_{2}$ is
A $1 : 9$
B $1 : 3$
C $3 : 1$
D $9 : 1$
Question 2 - Select One or More
Two light trollwys of masses $m_{1}$ and $m_{2} (= 3 m_{1})$ are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.

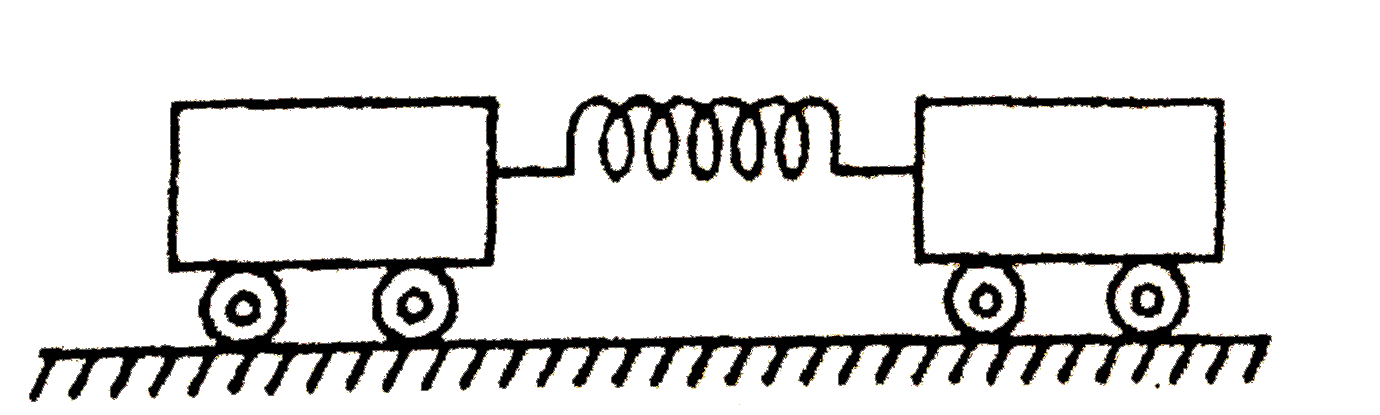AThe relationship between the velocties $v_{1}$ and $v_{2}$ of the trolleys is $v_{1} / v_{2} = 3$
BThe relationship between the periods $t_{1}$ and $t_{2}$ during which the trolleys move $t_{1} / t_{2} = 3$
CThe relationship between the distance $s_{1}$ and $s_{2}$ travelled by the trolleys is $s_{1} / s_{2} = 3$
DThe relationship between the force of friction $f_{1}$ and $f_{2}$ acting on the two trolleys is $f_{1} / f_{2} = \frac{1}{3}$
Question 3 - Select One
A mass $m$ is attached to a spring. The spring is stretched to $x$ by a force $F$ and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, $μ_{k}$ , is $: -$

A $μ_{k} = \frac{2 K x}{m g}$
B $μ_{k} = \frac{2 m g}{F}$
C $μ_{k} = \frac{F}{2 m g}$
D $μ_{k} = \frac{m g}{2 K x}$

The correct Answer is:D

$m v_{1} = 3 m v_{2} \Rightarrow v_{1} = 3 v_{2}$
Distance traveled by $m$ ,
$0 = v_{1}^{2} - 2 μ g s_{1}$ (i)
Distance traveled by $3 m$ ,
$0 = v_{2}^{2} - 2 μ g s_{2}$ (ii)
$\frac{s_{1}}{s_{2}} = {(\frac{v_{1}}{v_{2}})}^{2} = {(3)}^{2} = 9$

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two light trollwys of masses $m_{1}$ and $m_{2} (= 3 m_{1})$ are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.

A mass $m$ is attached to a spring. The spring is stretched to $x$ by a force $F$ and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, $μ_{k}$ , is $: -$

CP SINGH-CENTER OF MASS-Exercises

Two trolleys of mass m and 3m are attached by a spring. The spring was compressed and then released , they move off in opposite direction and comes to rest after covering distances s1 and s2 respectively. Assuming the coefficient of friction to be uniform , the ratio of distances s1:s2 is

The correct Answer is:D

mv1=3mv2⇒v1=3v2 Distance traveled by m , 0=v21−2μgs1 (i) Distance traveled by 3m , 0=v22−2μgs2 (ii) s1s2=(v1v2)2=(3)2=9

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two light trollwys of masses m1 and m2(=3m1) are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.

A mass m is attached to a spring. The spring is stretched to x by a force F and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, μk , is :−

CP SINGH-CENTER OF MASS-Exercises

$m v_{1} = 3 m v_{2} \Rightarrow v_{1} = 3 v_{2}$
Distance traveled by $m$ ,
$0 = v_{1}^{2} - 2 μ g s_{1}$ (i)
Distance traveled by $3 m$ ,
$0 = v_{2}^{2} - 2 μ g s_{2}$ (ii)
$\frac{s_{1}}{s_{2}} = {(\frac{v_{1}}{v_{2}})}^{2} = {(3)}^{2} = 9$

Two light trollwys of masses $m_{1}$ and $m_{2} (= 3 m_{1})$ are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.

A mass $m$ is attached to a spring. The spring is stretched to $x$ by a force $F$ and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, $μ_{k}$ , is $: -$