A charge q of mass m is projected form a long distance with speed v towards another stationery particle of same mass and charge the distance of closet approach of the particles is
q22πε0mv2
2q2πε0mv2
3q22πε0mv2
q2πε0mv2
The correct Answer is:D
As the first particle approaches the second due to repulsion it recedes away from it along the same line of approach.The seperation between them is minimum when their velocities are equal .Applying conservation of linear momentum
mv=mvf+mvfvf=V/2
⇒12mv2=12(m+m)v2f+q24πε0r
12mv2=122mv24+q24πε0r14mv2=q24πε0r
r=q2πε0mv2
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage II
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
A charged particle +q of mass m is placed at a distance d from another charge particle −2q of mass 2m in a uniform magnetic field of induction vectro B as shown in the fig.If the particles are projected towards each other with equal speeds v.(Neglect the interaction between the particles)
(a)Find the maximum value of the projection speed Vmax so that the two particles do not collide.
b)Find the time interval after which collision occurs between the particles if projection speed equals 2Vmax
(c)In the previous part,assuming that the particles stick after the collision find the radius of the circular path of the particle in subsequent motion.

View SolutionA particle (A) having charge Q and mass m is at rest and is free to move. Another particle (B) having charge q and mass m is projected from a large distance towards the first particle with speed u. (a) Calculate the least kinetic energy of the system during the subsequent motion. (b) Find the final velocity of both the particles. Consider coulomb force only.
View Solution
Knowledge Check
A particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
What are the speeds of particles P and Q, when their separation is minimum ?Av02,v02B0,vCv03,2v03D0,0A particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation isA14πε0q2r+12mv20B−14πε0q2r+12mv20C14πε0q2r−mv204D−14πε0q2r+mv204A particle of mass m moving towards the east with speed v collides with another particle of the same mass and same speed v moving towards the north. If the two particles stick to each other, the new particle of mass 2m will have a speed of
AvBv2Cv√2Dv√2
Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
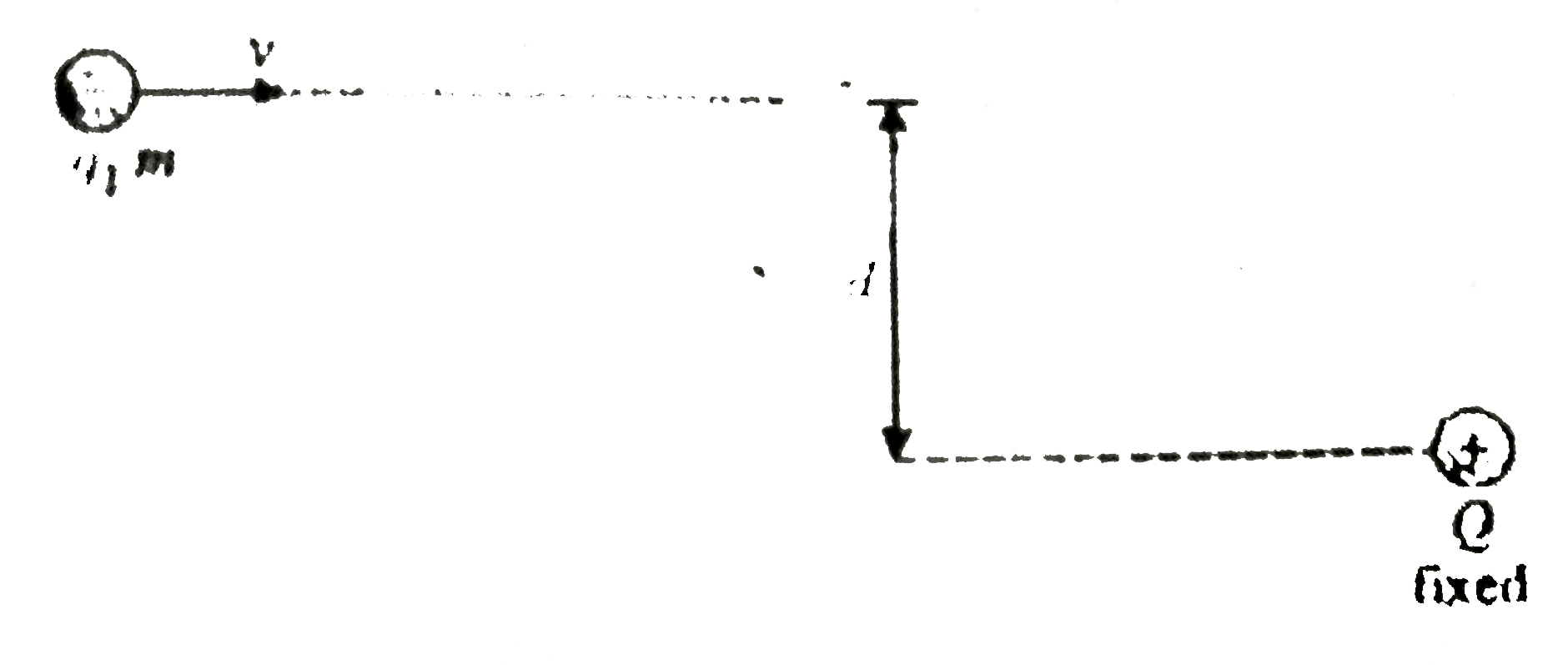
View SolutionThe closed distance of approach of an α− particle travelling with velocity V towards a stationary nucleus is d.For the closest distance to become d3 towards a stationary nucleus of double of the charge,the velocity of projection of the α− particle has to be
View SolutionA particle of mass M and charge q , initially at rest , is accelerated by a uniform electric field E through a distance D and is then allowed to approach a fixed static charge Q of the same sign . The distance of the closest approach of the charge q will then be
View SolutionThe closed distance of approach of an α− particle travelling with velocity V towards a stationary nucleus is d.For the closest distance to become d3 towards a stationary nucleus of double of the charge,the velocity of projection of the α− particle has to be
View SolutionWhen an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
View Solution
