If a straight conductor of length 40cm bent in the form of a square and the current 2A is allowed to pass through square, then find the magnetic induction at the centre of the square loop.
Bnet=4Bside
Bnet=4μ04π×IL/2(sin45∘+sin45∘)
=4Xμ04π×IL/2(√2)=μ04π8√2IL
=10−7×8√2×2×10=16√2μT

Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:C.U.Q-KEY
Explore 121 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-I(C.W)
Explore 58 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionTwo identical wires each of length L are bent to form a circular loop and a square loop. If the same current i flows in the two wires, then the ratio of the magnetic inductions at the centre of the circular and square loops is :
View Solution
Knowledge Check
An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
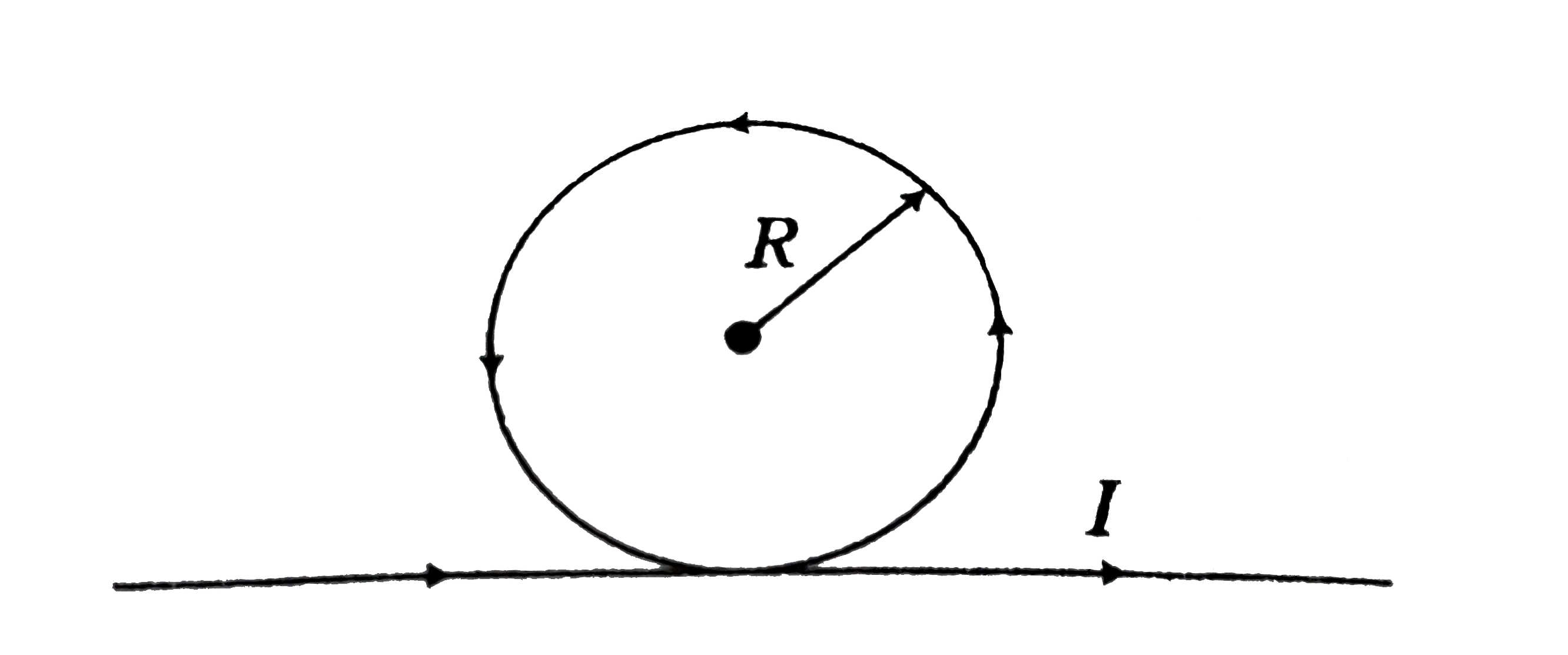 AZeroBinfinityCμ04π2ir(π+1)TeslaDμ04π2ir(π−1)Tesla
AZeroBinfinityCμ04π2ir(π+1)TeslaDμ04π2ir(π−1)TeslaAn infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of i ampere and the radius of the circular loop is V metre. The magnetic induction at the centre of the circular part is-
 Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)
Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)ABCD is a square of side L. A very long straight conductor carrying a current i passes through the vertex A of the square and is perpendicular to its plane. The minimum magnetic induction at a vertex of the square is
Aμ04π2√2iLBμ04π√2iLCμ04π4√2iLDμ04π2iL
A wire of length l is bent in the form of a square and carries a current I. What is the value of its magnetic moment?
View SolutionAn infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
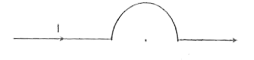
View SolutionTwo persons A and B took a wire of equal length 'A' bent in the form of a reactangle with perimeter 12 cm. B bet it in the form of a square, then find the area of the square , then find the area of the square formed.
View SolutionA wire of length 10cm is bent into an arc of a circle such that it subtends an angle of 1 radian at the centre. If a current of 1A is passed through the wire, the magnetic induction at the centre of the circle will be
View SolutionA square loop of side a carries a current I. The magnetic field at the center of the loop is
View Solution
