A particle of charge +q and mass m moving under the influnce of a uniform electric field Eˆiand a uniform magnetic field Bˆk follows trajectory from P to Q as shown in figure. The velocities at P and Q vˆi and −2vˆj respectively. Which of the following statement(s) is/are correct
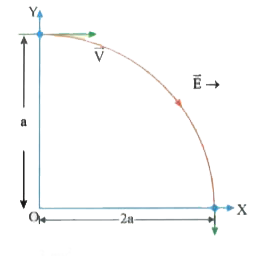
E=34mv2qa
Rate of work done by electric field at Pis 34mv3a
Rate of work done by electric field at P is zero
Rate of work done by both the fields at Q is zero
The correct Answer is:A, B, D
Kinetic energy of the particle at point P=12mv2
K.E of the particle at point Q=12m(2v)2
Increase in K.E =32mv2
It comes from the work done by the electric force qE on the particle as it covers a distance 2a along the x - axis .
Thus 32mv2=qE×2a⇒E=34mv2qa
The rate of work done by the electric field at P=F×v=qE×v=34mv2a
At Q, →F=q→E is along x - axis while velocity is along negative y - axis . Hence create of work done by electric field =→F.→v=0(∵=90∘) . similarly , according to equation →Fm=q(→v×→B) force →Fm is also perpendicular to velocity vector →v
Hence the rate of work done by the magnetic field = 0 .
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 3
29 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A particle of charge +q and mass m moving under the influence of as uniform electric field Eˆi and uniform magnetic field Bˆk follows trajectory form P to Q as shown in figure. The velocities at P and Q re vˆiand−2ˆj. Which of the following statement(s) is/are correct?
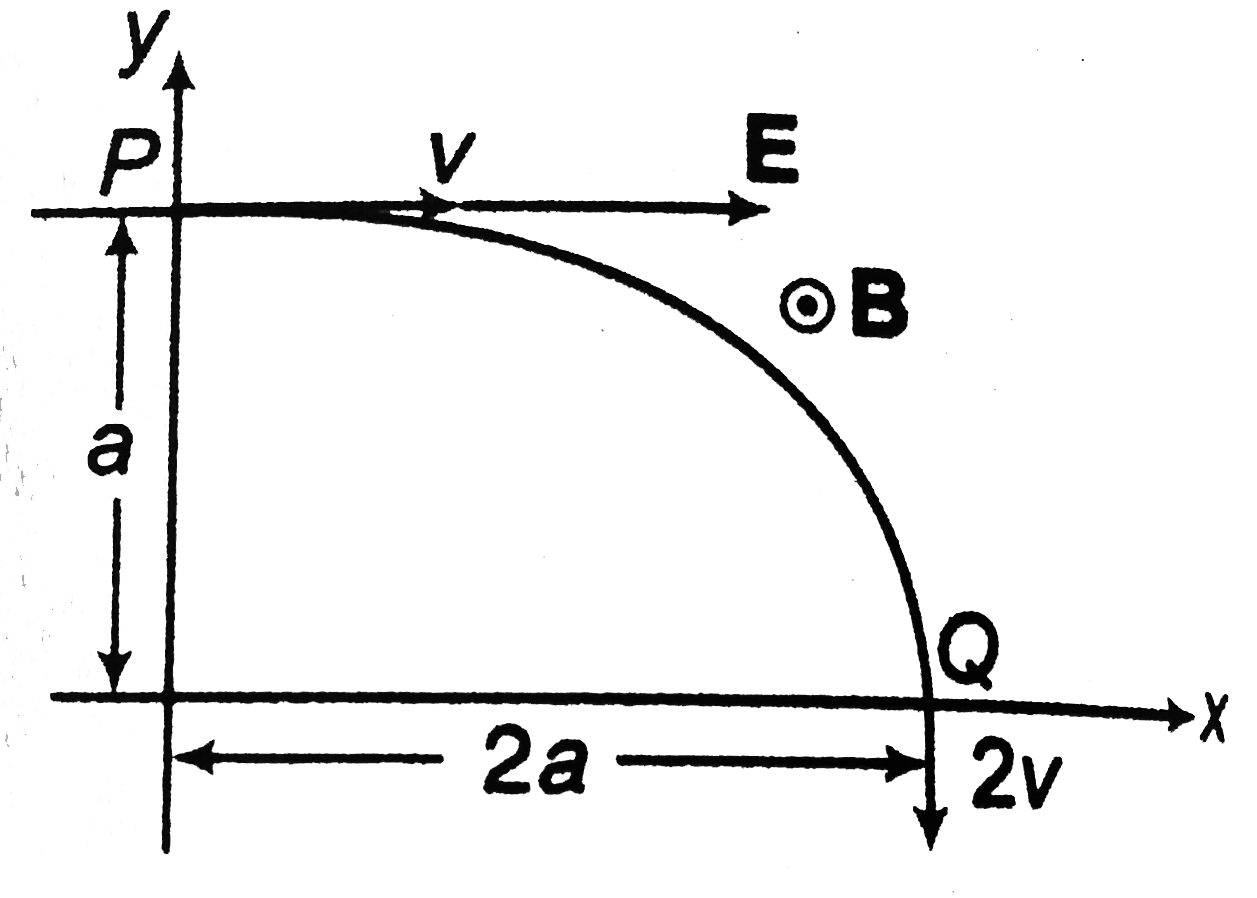
a.E=34[mv2qa]
b. Rate of work done by the electrif field at P is 34[mv3a]
c. Rate of work done by the electric field at P is zero.
d. Rate of work done by both the field at Q is zero.
View SolutionA particle of charge +q and mass m moving under the influence of a uniform electric field Eˆi and a magnetic field Bˆk enters in I quadrant of a coordinate system at a point (0,a) with initial velocity vˆi and leaves the quadrant at a point
(2a.,0) with velocity −2vˆj Find
(aq) Magnitude of electric field at point (0,a) (C ) Rate of work done by both the fields at (2a,0) .
View Solution
Knowledge Check
A particle of charge +q and mass m moving under the influence of a uniform electric field Eˆi and uniform magnetic field Bˆk follows a trajectory from P→Q as shown in fig. The velocities at PandQ are vˆi and −2vˆj . which of the following statement(s) is/are correct ?
 AE=34[mv2qa]BRate of work done by the electric field at P is 34[mv3a]CRate of work done by the electric field at p is zeroDRate of work done by the electric field at Q is zero
AE=34[mv2qa]BRate of work done by the electric field at P is 34[mv3a]CRate of work done by the electric field at p is zeroDRate of work done by the electric field at Q is zeroA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
A25mv20qE0B100mv20qB0C50mv20qE0D14mv20qE0A particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
A25mv20qE0B100mv20qB0C50mV20qE0D14mv20qE0
A charged particle is moving in a circular path in uniform magnetic field. Match the following.

View SolutionA particle of charge q=4μC and mass m = 10 mg starts moving from the origin under the action of an electric field →E=4ˆi and magnetic field →B=(0.2T)ˆk. Its velocity at (x, 3, 0) is (4→i+3→j). The value of x is -
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View SolutionA particle of charge q and mass m is moving along the x-axis with a velocity v and enters a region of electric field E and magnetic field B as shown in figures below. For which figure the net force on the charge may be zero?
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View Solution
