A horizontal magnetic field B is produced across a narrow gap between the two square iron pole pieces. A closed square loop of side a, mass m and resistance R is allowed to fall with the tope the lopp in the field. The loop attians a terminal velocity equal to :

Induced emf in the loop, when it is falling with terminal velocity
e=BVa, i=eR=BvaR
Vertically upward force experienced by loop due to this
F=Bia , B(BvaR)a, =B2va2r
When the loop attains velocity 'v'
mg=B2va2R, V=mgRB2a2
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - C.U.Q 1
51 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Assertion & Reason
11 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
A magnetic field B=B0(y/a)(^)k is into the paper in the +z direction, B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
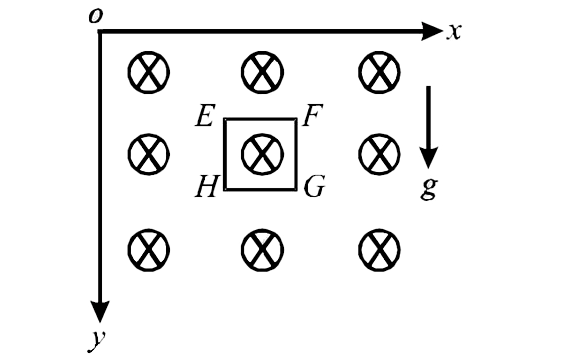
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.
View SolutionA region of width L contains a uniform magnetic field B directed into the plane of the figure. A square conducing loop of side length l(<L) is kept with its side AB at the boundary of the field region (see Figure). The loop is pushed into the field region with a speed such that it just manages to exit the field region. Calculate the time needed for the entire loop to enter the field region after it is pushed. Mass and resistance of the loop is M and R respectively.
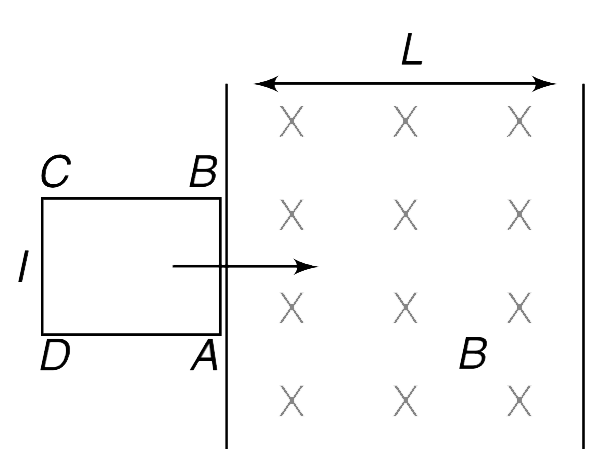
View Solution
Knowledge Check
A square loop of side a and resistance B is moved in the region of uniform magnetic field B (loop remaining completely inside field), with a velocity v through a distance x. The work done is
ABt2vxRBB2t2vxRC4B2t2vxRDNone of the aboveA square loop of side a and resistance R is moved in the region of uniform magnetic field B(loop remaining completely insidefield), with a velocity v through a distance x. The work done is:
ABl2vxRB2B2l2vxRC4B2l2vxRDnonePQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will beA(i) Ba2 (ii) Bav2R (iii) B2a2v24R2B(i) Ba2 (ii) zero (iii) zeroC(i) Ba2 (ii) Bav2R (iii) zeroD(i) zero (ii) zero (iii) zero
A square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
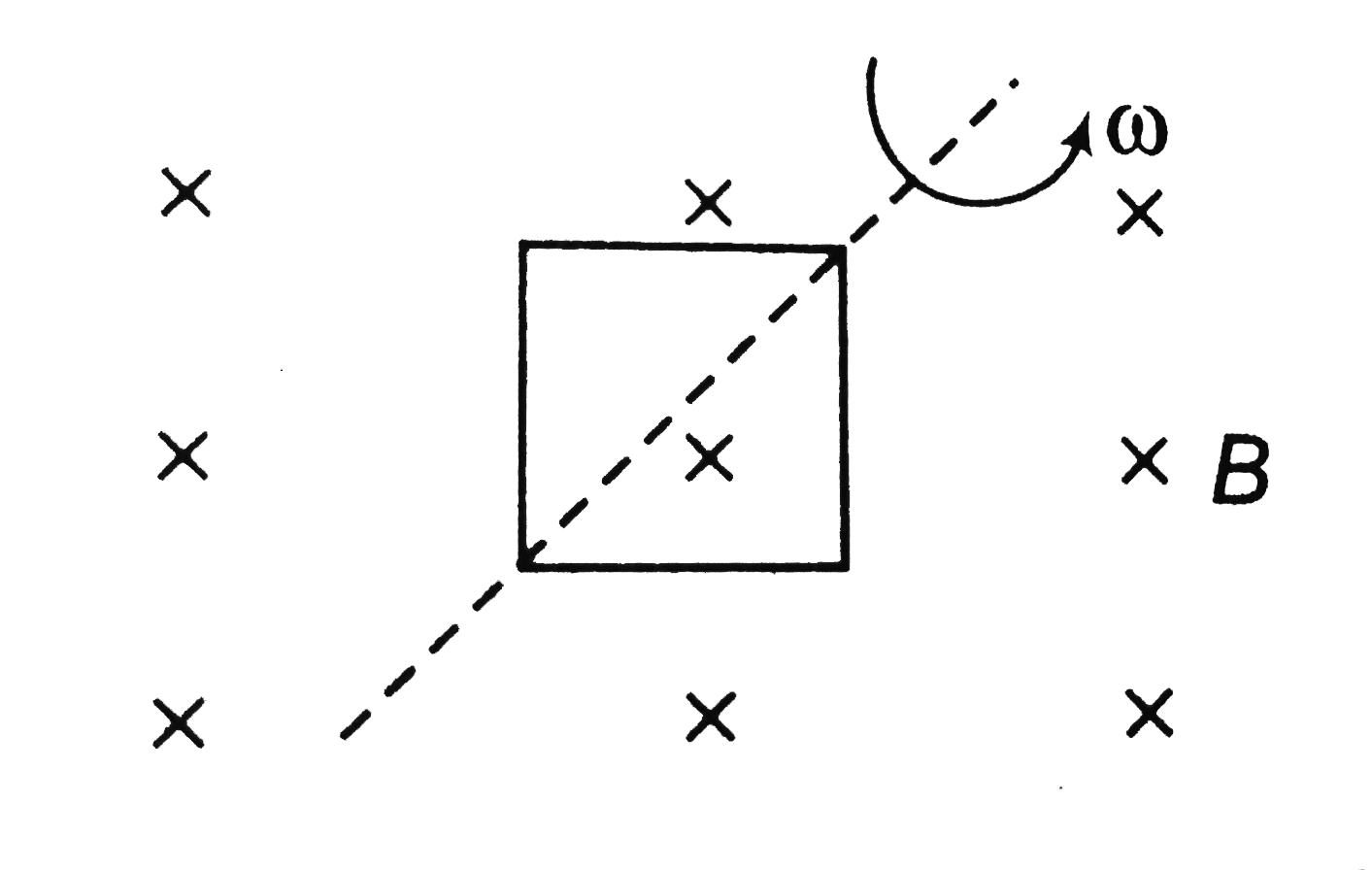
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

External force required to maintain constant velocity of the loop for x=−95a will be
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=−9a/5, magnitude of induced current and its direction as seen from above will be:
View SolutionA square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
View SolutionA rectangular loop of resistance R, and sides l and X, is pulled out of a uniform magnetic field B with a for maintaining uniform velocity of withdrawal is __
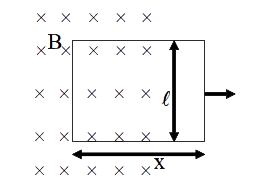
View Solution
