Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.

The maximum current in the indcutor is :
3V02√3CL
V0√3CL
2V0√3CL
V0√CL
The correct Answer is:A
Loss in energy of capacitor = Energy store in inductor
⇒12VC20+123C(2V0)2−12×4CV2=12LI
⇒I=32V0√3V0L
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -VI13videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Integer type questions2videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -V11videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -443videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)14videos
ELECTRO MAGNETIC WAVES
Similar Questions
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum isView SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum isView Solution
Knowledge Check
- Question 1 - Select One
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
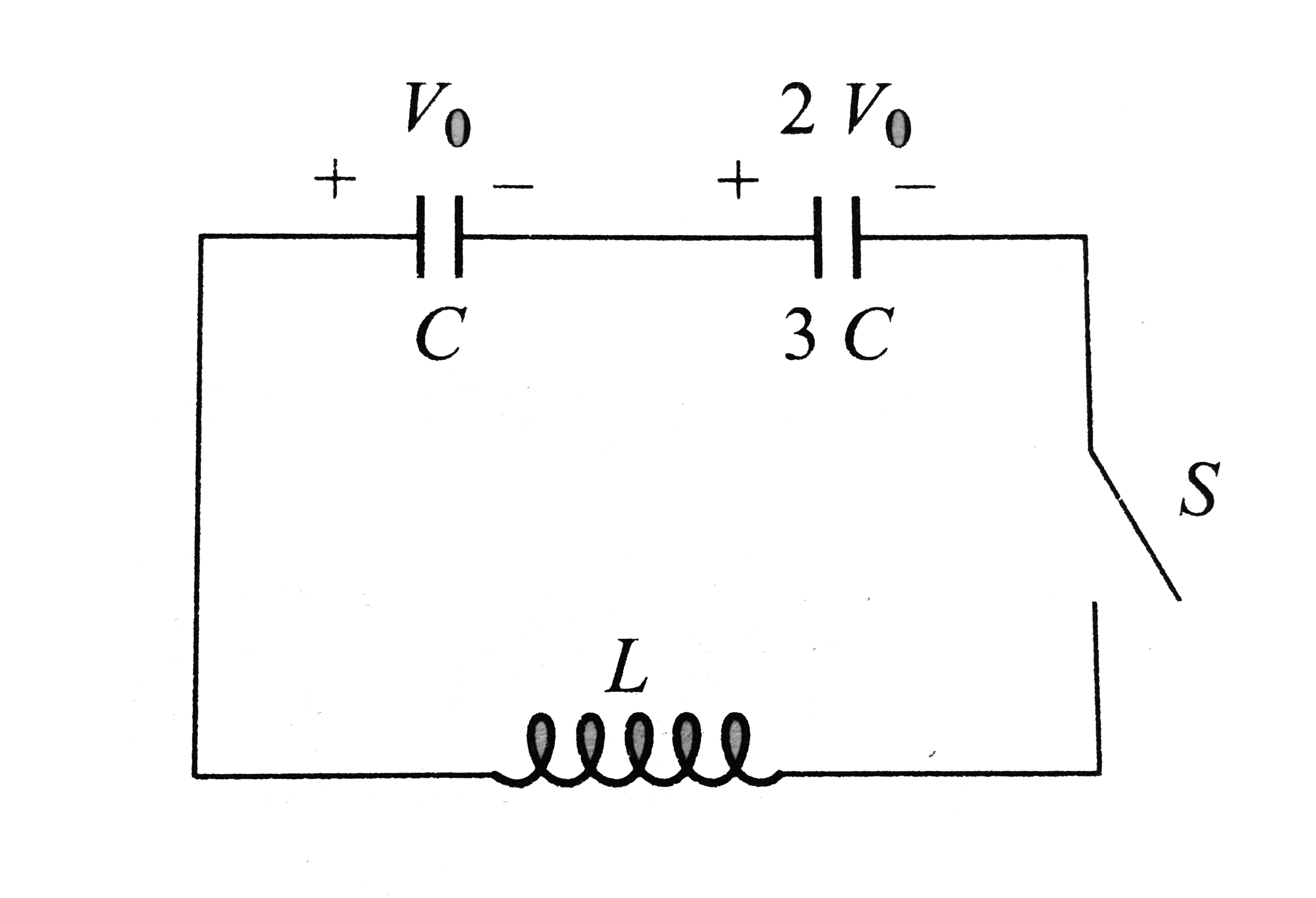
The maximum current in the inductor isA3V02√3CLBV0√3CLC2V0√3CLDV0√CL - Question 2 - Select One
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
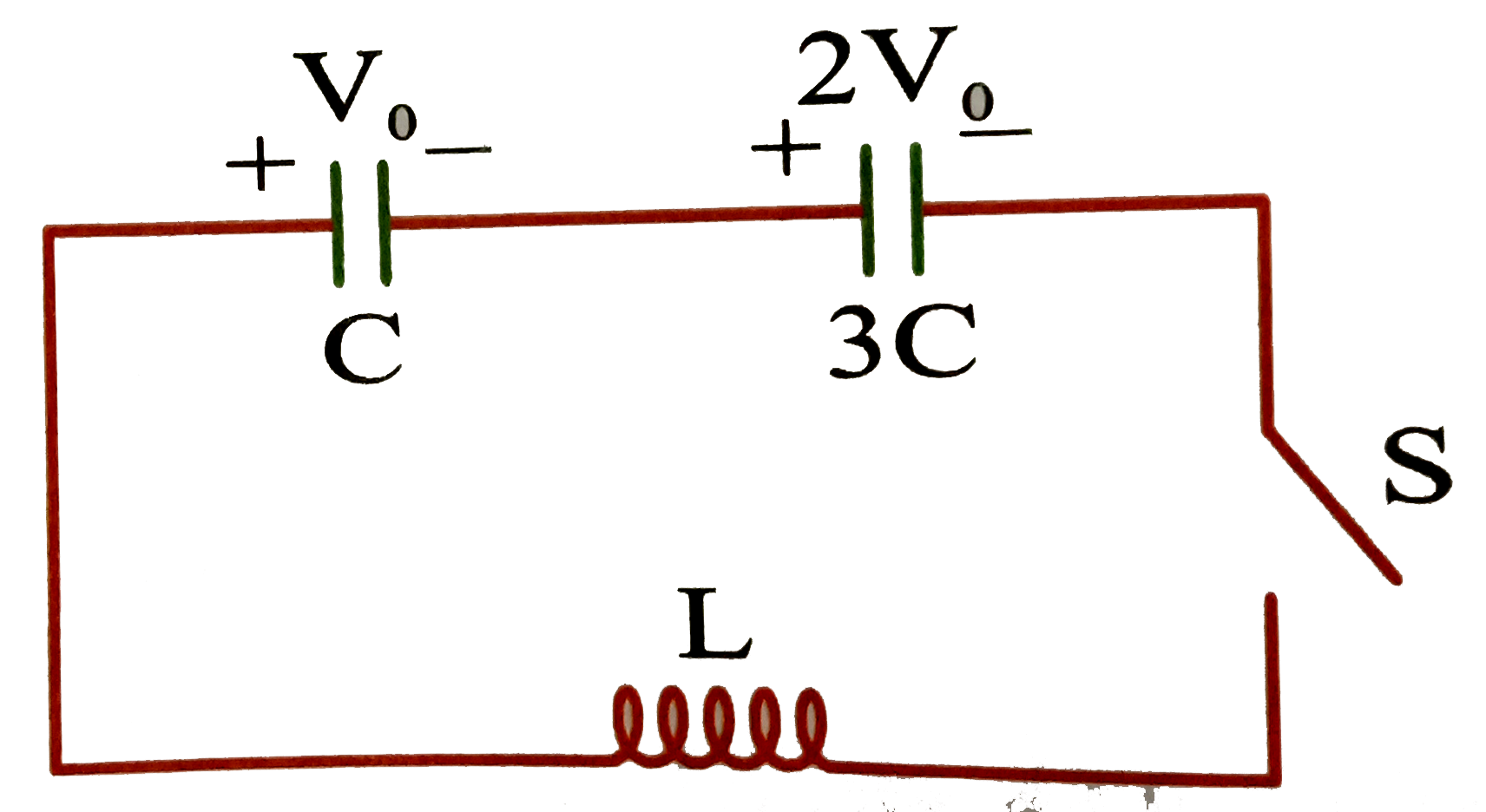
Potential difference across capacitor of capacitance 3C when the current in the cirucit is maximum is :AV04BV04C5V04D7V04 - Question 3 - Select One
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
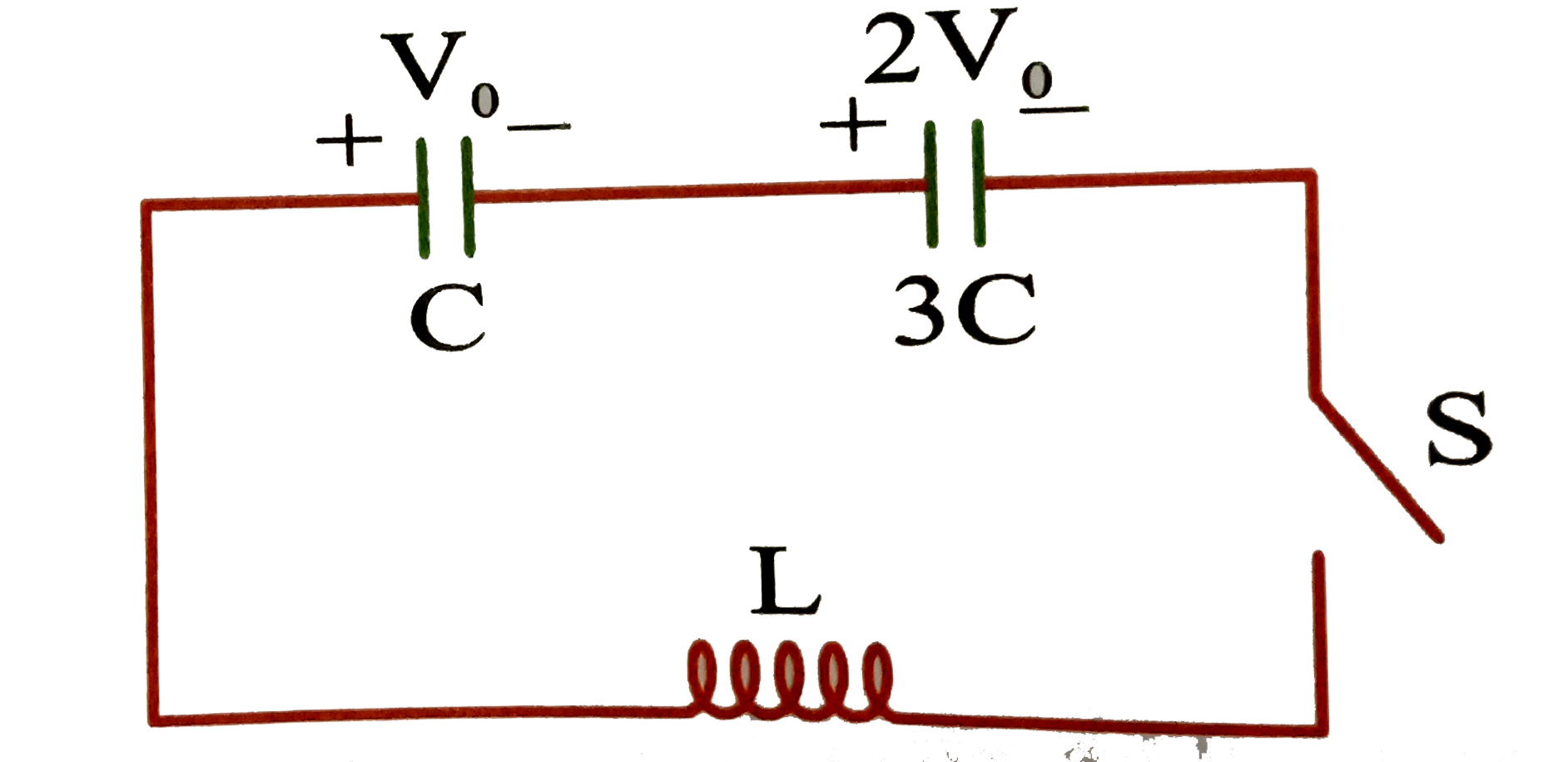
Potential difference across capacitor of capacitance C when the current in the cirucit is maximum isAV04B3V04C5V04D7V04
Two capacitors 2C and 4C initially charged to potential difference of V0and3V0 with the potential as show are connected to an inductor of inductance L. Initial curren tin the inductor is zer. Now the swtich 'S' is closed. The maxmimum current in the circuit is
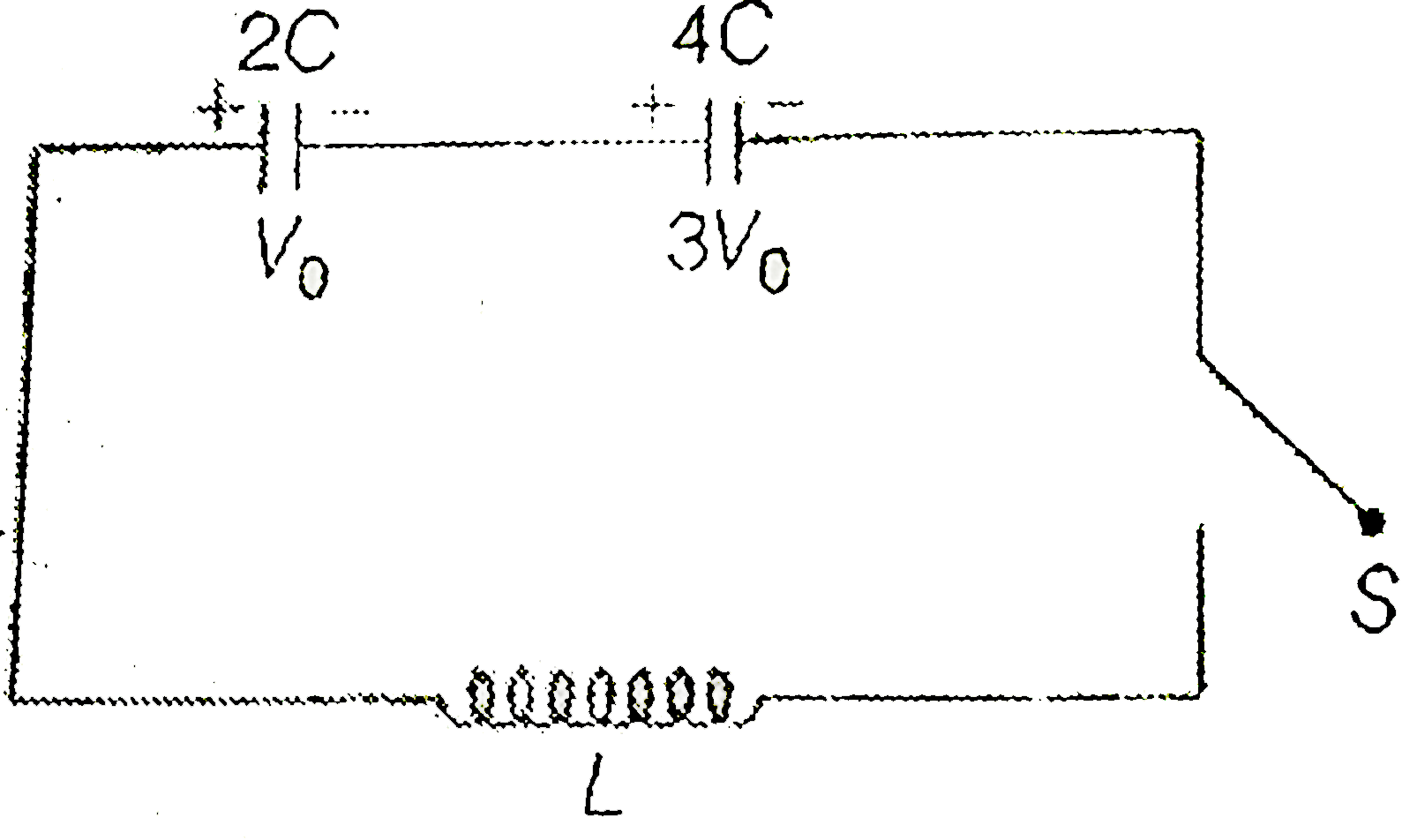 View Solution
View SolutionA capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then
 View Solution
View SolutionIn the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4ɛ and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
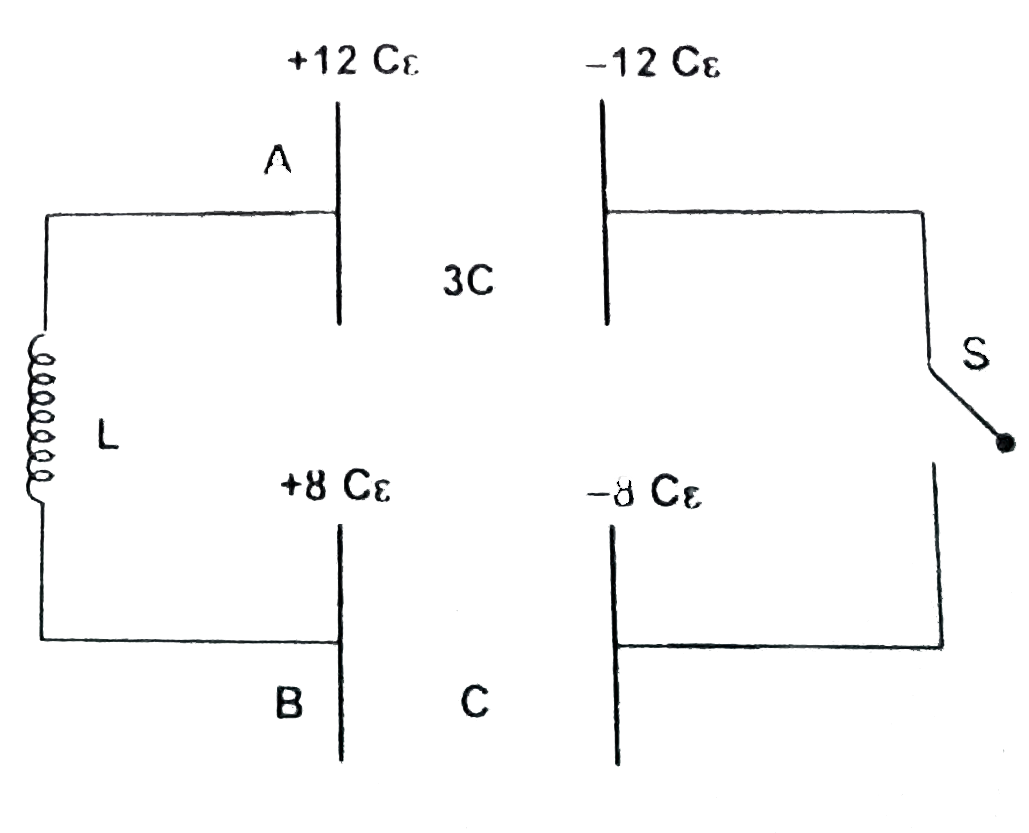 View Solution
View SolutionA capacitor having capacitance 2 μF is charged to a potential difference of 50 V. it is then diconnected from battery and connected to an inductor of inductance 5 mH. Peak current that flows through the inductor is
View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View Solution

