Question

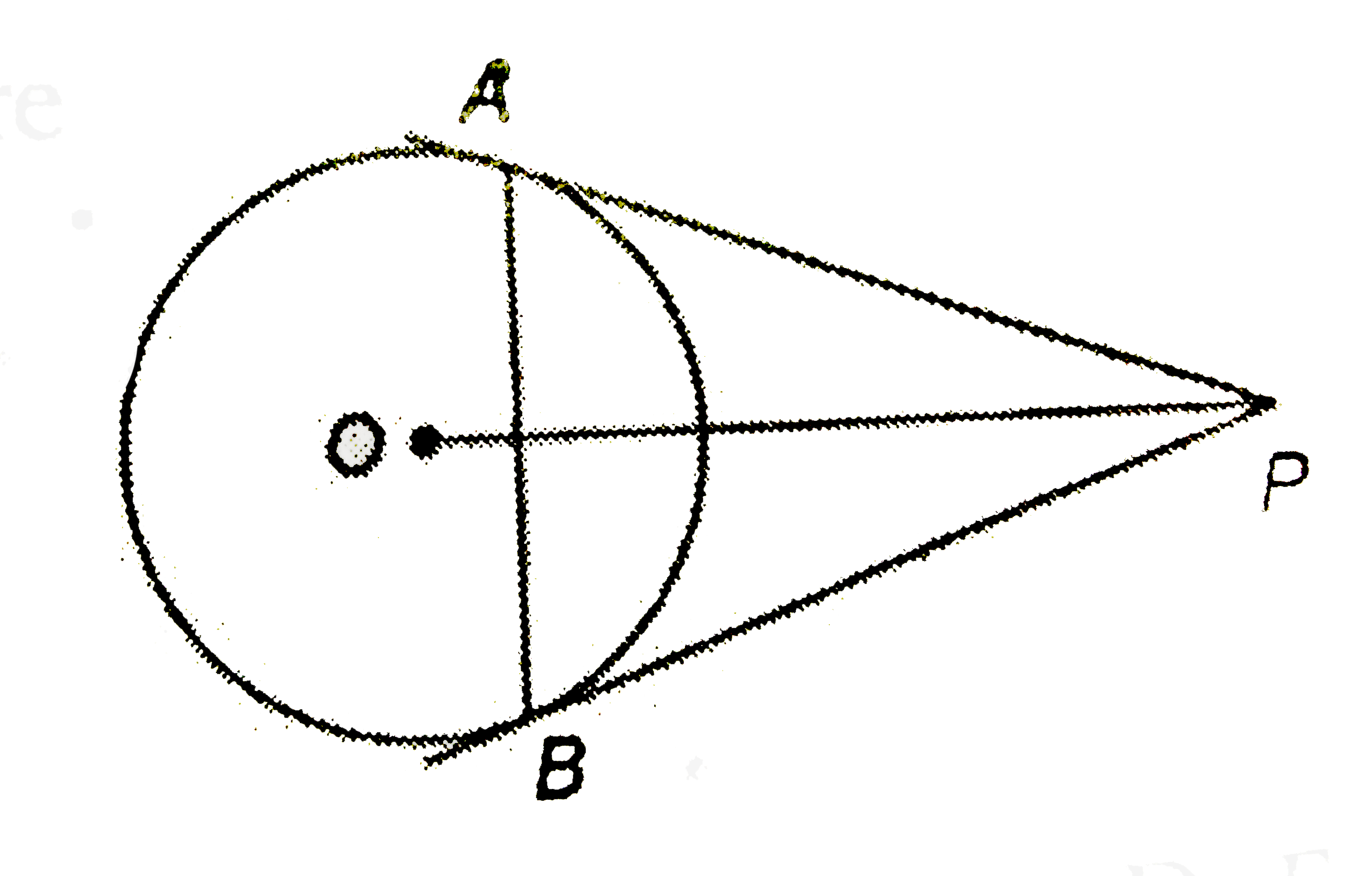
From an external point $P,$
two tangents $PAandPB$
are drawn to the circle with centre $O\stackrel{.}{}$
Prove that $OP$
is the perpendicular bisector of $AB\stackrel{.}{}$

Explanation

In `triangle PAC` and `triangle PBC`


`PA=PB` [length of tangents drawn from external point are equal]


`angle APC =angle BPC` [As, PA and PB are equally inclined to OP]


PC= PC [Common]


Therefore, by SAS criteria of similarity


`Delta PAC cong triangle PBC`


`Rightarrow AC =BC and angle ACP=angle BCP`


` angle ACP+angle BCP=180^{circ}`


So,` angle ACP+angle BCP=90^{circ}`


Therefore, `OP bot AB`