AC is tangent to O, O'D is ⊥ to AC, Find the value of DO'CO
Step by step video & image solution for AC is tangent to O, O'D is _|_ to AC, Find the value of (DO')/(CO) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
AC is tangent to O, O'D is ⊥ to AC, Find the value of DO'CO
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View Solution
Knowledge Check
In the figure, ABC is a triangle in which AB=AC. A circle through B touches AC at D and intersects AB at P. If D is the mid - point of AC, Find the value of AB :
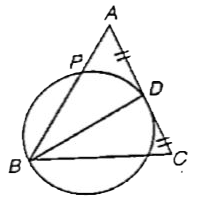 A2APB3APC4APD4√2cm
A2APB3APC4APD4√2cmIn a circle O is the centre and ∠COD is right angle. AC=BDandCD is the tangent at P. What is the value of AC+CP, if the radius of the circle is 1 metre?
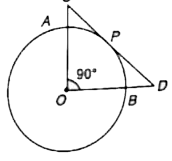 A105 cmB141.4 cmC138.6 cmDcan't be determined
A105 cmB141.4 cmC138.6 cmDcan't be determinedAB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the ∠BDOis
A60∘B90∘C45∘D75∘
. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View SolutionIn the given figure O is the centre of the circle and AB is a tangent at B. If AB=15 cm and AC=7.5 cm, find the rdius of the circle.

View SolutionIf ABCDEF is a regular hexagon inscribed in a circle with centre O, then the value of ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF equals
View Solution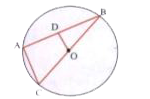
In the above diagram, BC is diameter, O is centre and OD⊥AB. If AC=λOD, then value of λ is
View Solution
