. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
To solve the problem, we will follow these steps:
Step 1: Understand the Configuration
We have two equal circles with centers O and O' that touch each other at point X. The line OO' is extended to point A, which is outside the circle centered at O'. A tangent line AC touches the circle centered at O at point C. The line O'D is perpendicular to AC.
Step 2: Define the Radii
Let the radius of both circles be r. Therefore:
- OX = r
- O'X = r
Since the circles are equal, we have:
- AO' = O'X + OX = r + r = 2r
Step 3: Establish Relationships
From the configuration, we can see that:
- AO = OX + AX = r + AX
- Since AO' = 2r, we can express AX as:
AO=OX+AX=r+AX⟹AX=AO−OX=2r−r=r
Step 4: Use Similar Triangles
Now, we analyze triangles AOD and AOC:
- Triangle AOD is similar to triangle AOC because:
- Angle O'DA = Angle OCA (both are right angles)
- Angle AOD = Angle AOC (common angle)
From the similarity of triangles, we have:
DO′CO=O′AOA
Step 5: Calculate the Lengths
We already established:
- O'A = AO' = 2r
- OA = AO = 3r (since AO = OX + AX = r + r + r)
Step 6: Substitute the Values
Substituting the lengths into the ratio gives:
DO′CO=O′AOA=2r3r=23
Step 7: Final Result
Thus, the value of DO′CO is:
DO′CO=23
We have two equal circles with centers O and O' that touch each other at point X. The line OO' is extended to point A, which is outside the circle centered at O'. A tangent line AC touches the circle centered at O at point C. The line O'D is perpendicular to AC.
Let the radius of both circles be r. Therefore:
- OX = r
- O'X = r
- AO' = O'X + OX = r + r = 2r
From the configuration, we can see that:
- AO = OX + AX = r + AX
- Since AO' = 2r, we can express AX as:
AO=OX+AX=r+AX⟹AX=AO−OX=2r−r=r
Now, we analyze triangles AOD and AOC:
- Triangle AOD is similar to triangle AOC because:
- Angle O'DA = Angle OCA (both are right angles)
- Angle AOD = Angle AOC (common angle)
DO′CO=O′AOA
We already established:
- O'A = AO' = 2r
- OA = AO = 3r (since AO = OX + AX = r + r + r)
Substituting the lengths into the ratio gives:
DO′CO=O′AOA=2r3r=23
Thus, the value of DO′CO is:
DO′CO=23
Topper's Solved these Questions
Similar Questions
In the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
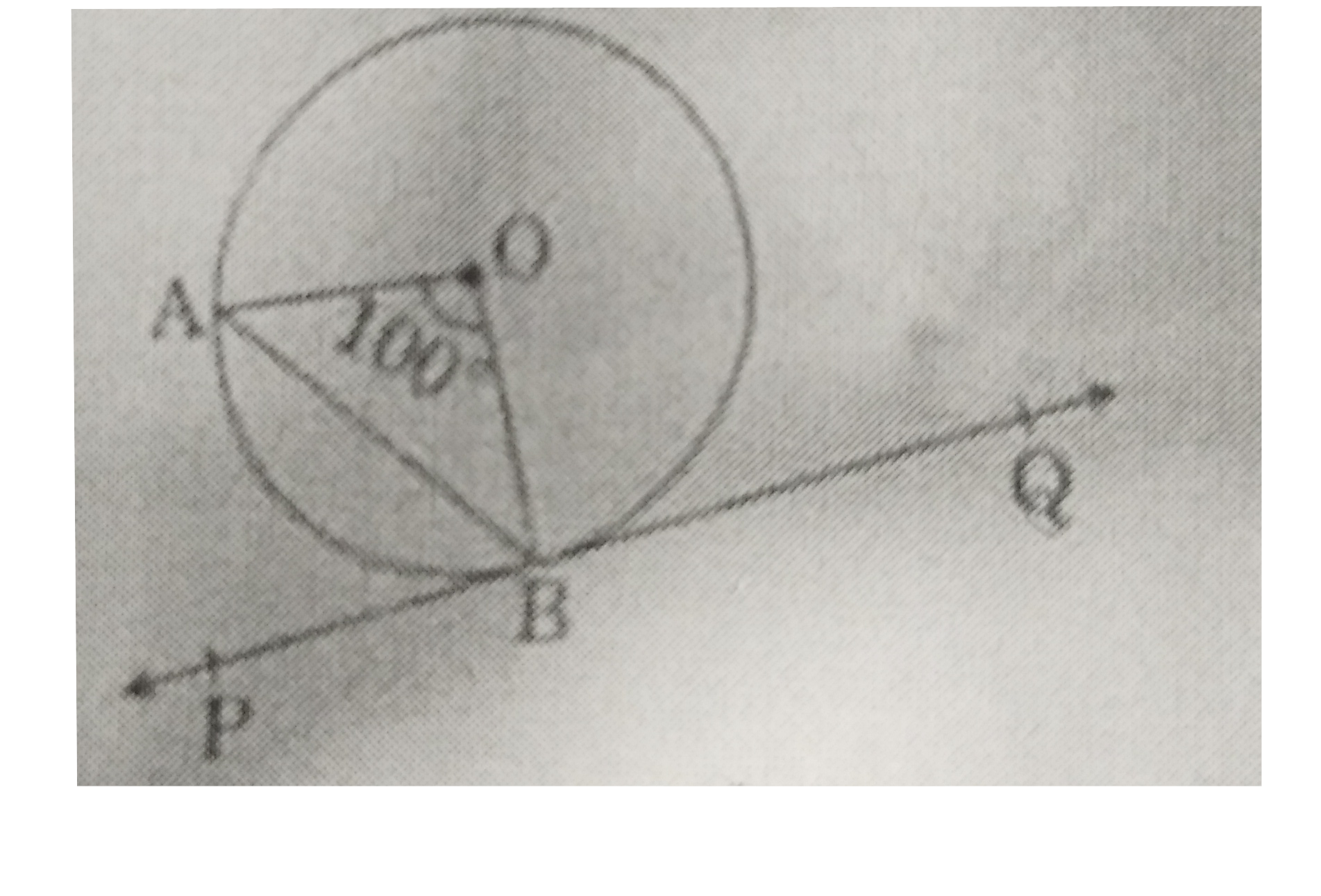
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠BOD .Is BD a diameter of the circle
View SolutionTwo circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.

View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
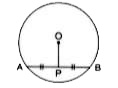
View SolutionThe given figure shows a circle with centre O. P is mid-point of chord AB.
Show that OP is perpendicular to AB.
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠BOC . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠COD . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠OCB . Is BD a diameter of the circle
View Solution
