The bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of △ABC at P as shown in the figure. If AP and BC produced meet at Q prove that CQ=CA.
From diagram
∠Q=x
∠CAQ is isoceles
CA=CQ.
Similar Questions
The bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P as shown in Figure. If AP and BC produced meet at Q,. prove that CQ=CA
View SolutionThe bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P as shown in Figure. If AP and BC produced meet at Q, prove that CQ=CA.
View SolutionThe bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
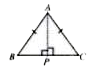
View SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
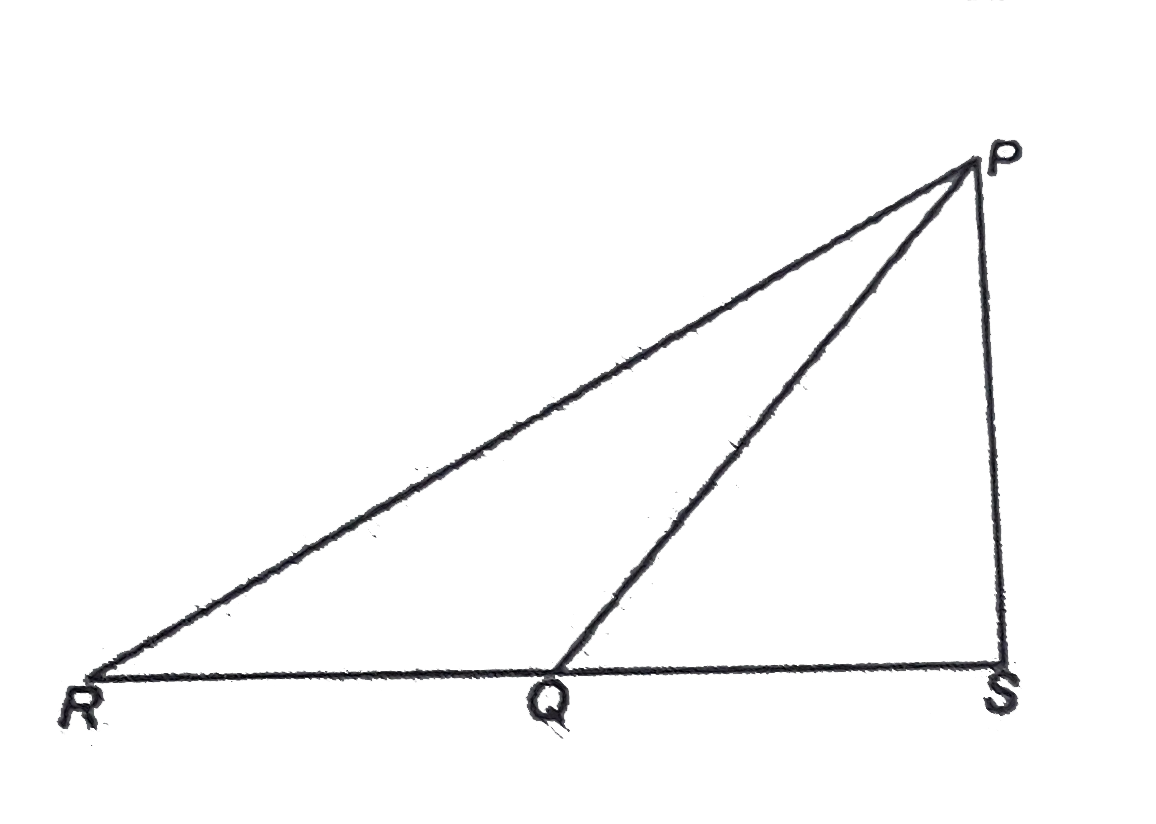
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionAn isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.
View SolutionThe bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionIn given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
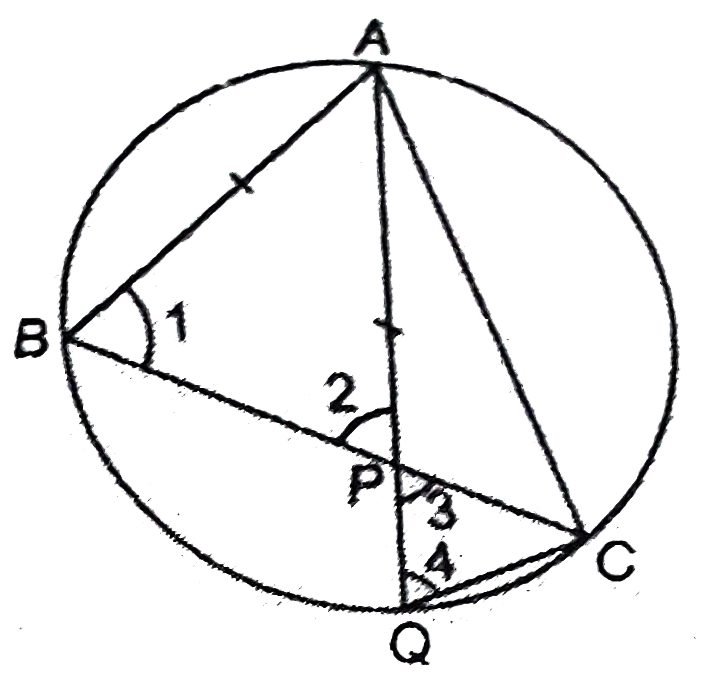
View Solution
