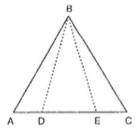
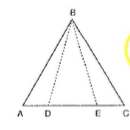
In Fig. 4.132, if AD⊥BC and BDDA=DADC , prove that ABC is a right triangle. (FIGURE)
Step by step video & image solution for In Fig. 4.132, if A D_|_B C and (B D)/(D A)=(D A)/(D C) , prove that A B C is a right triangle. (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
In Fig. 5.10, if AC=BD, then prove that AB=CD.
 View Solution
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.
 View Solution
View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
 View Solution
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14ACView SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE
 View Solution
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View Solution

