Question

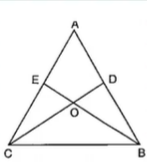
In Fig.
4.133, if $ABE\cong ACD$
, prove
that $ADEABC$
.
(FIGURE)

Explanation

To prove that triangle $$ADE$$ is similar to triangle $$ABC$$ given that triangle $$ABE$$ is congruent to triangle $$ACD$$, we can follow these steps:

1. Understanding Congruence: Since triangle \( ABE \) is congruent to triangle \( ACD \), we know that their corresponding sides are equal. Thus, we have:
\( AB = AC \quad \text{and} \quad AE = AD \)

2. Setting Up Proportions: From the congruence of triangles, we can set up the following proportion:
\( \frac{AB}{AC} = \frac{AD}{AE} \)

3. Rearranging the Proportions: We can rearrange the proportion to express it in a different form:
\( \frac{AB}{AD} = \frac{AC}{AE} \)

4. Identifying Common Angle: In triangles \( ADE \) and \( ABC \), we note that angle \( A \) is common to both triangles.

5. Applying the Side-Angle-Side (SAS) Similarity Criterion: We have established that:
- The ratios of two pairs of corresponding sides are equal:
\( \frac{AB}{AD} = \frac{AC}{AE} \)
- The angle \( A \) is common to both triangles.

By the Side-Angle-Side (SAS) similarity criterion, we can conclude that:
\( \triangle ADE \sim \triangle ABC \)

6. Conclusion: Therefore, we have proved that triangle \( ADE \) is similar to triangle \( ABC \).