In figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.


Using Pythagoras Theorem In ΔADC as ∠ADC=90°
AC2=AD2+DC2
AC2=AD2+[BC−BD]2
AC2=AD2+BD2+BC2−2BC.BD
AC2=AB2+BC2−2BC.BD [∵ In ΔADB, AB2=AD2+BD2]
Hence it is proved that AC2=AB2+BC2−2BC.BD
Topper's Solved these Questions
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:EXERCISE 6.3
Explore 16 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:Exercise 6.2
Explore 10 Videos
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:EXERCISE 13.2
Explore 8 Videos
Similar Questions
In figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn ABC, ∠A=60o . Prove that B C^2=A B^2+A C^2-A B.A C .
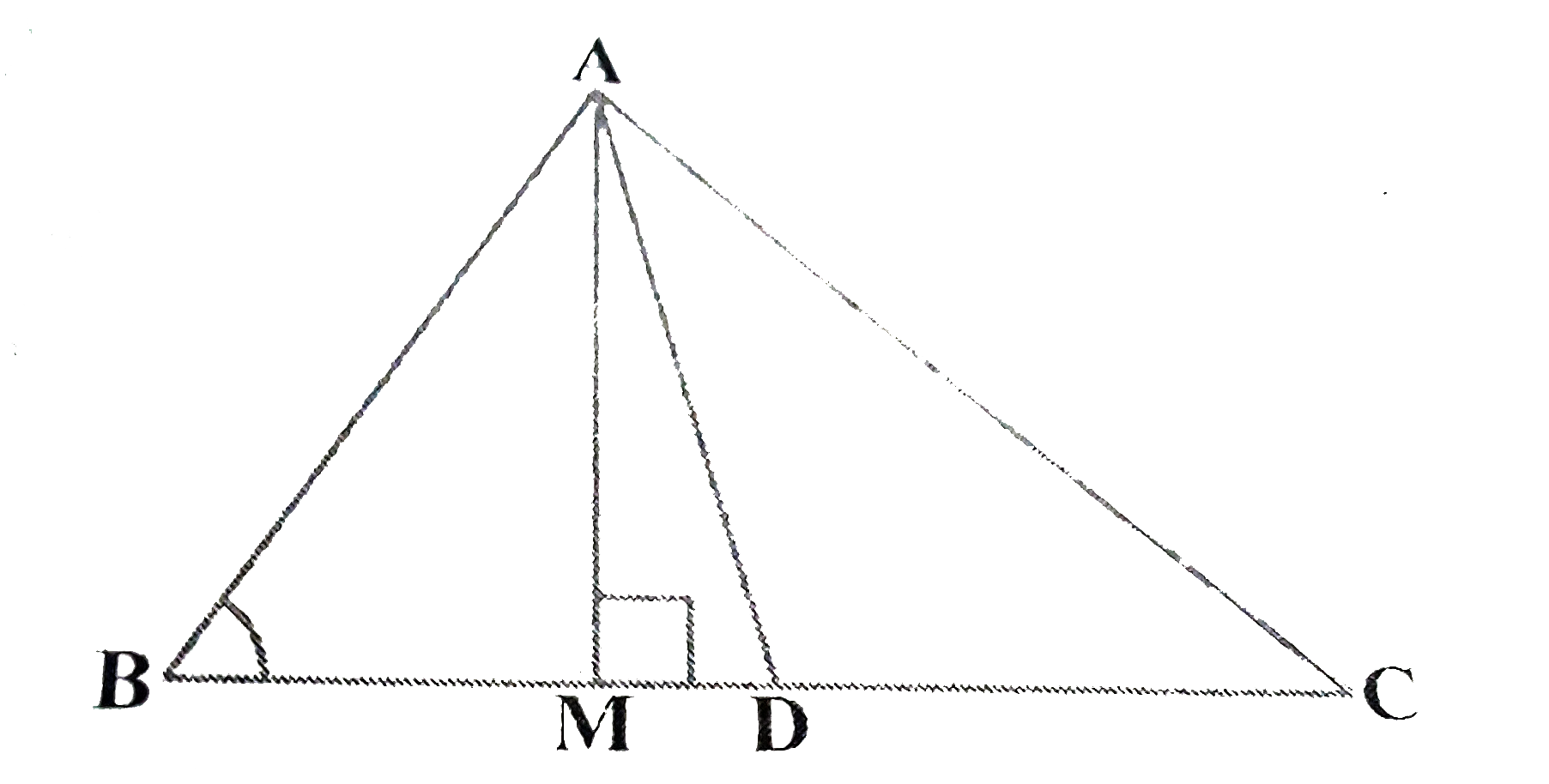
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
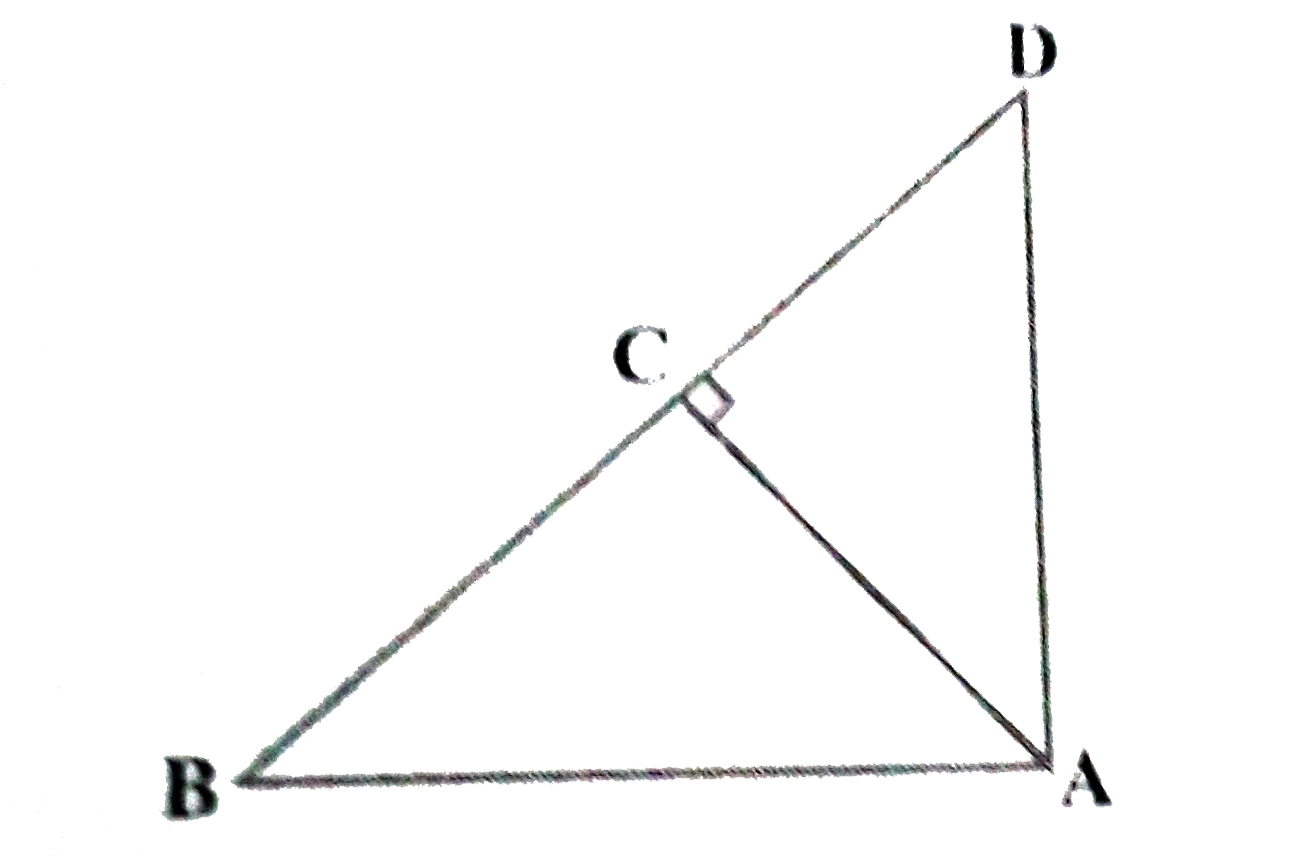
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2

View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View Solution