In an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
Video Solution
Text Solution
Given, equilateral triangle ABC,AD⊥BC
Since, it is an equilaateral triangle, the perpendicualr also bisects the side.
Hence,BD=DCorBD=(12)BC=(12)AB
Now, In△ABD, we have
AB2=AD2+BD2
AB2−BD2=AD2
BC2−BD2=AD2
(2CD)2−CD2=AD2
3CD2=AD2
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
(a+b+c−d)2−(a−b−c+d)2 =?
A2a(a+b+c)B4a(b+d−e)C2a(b+c−d)D4a(b−d+c)
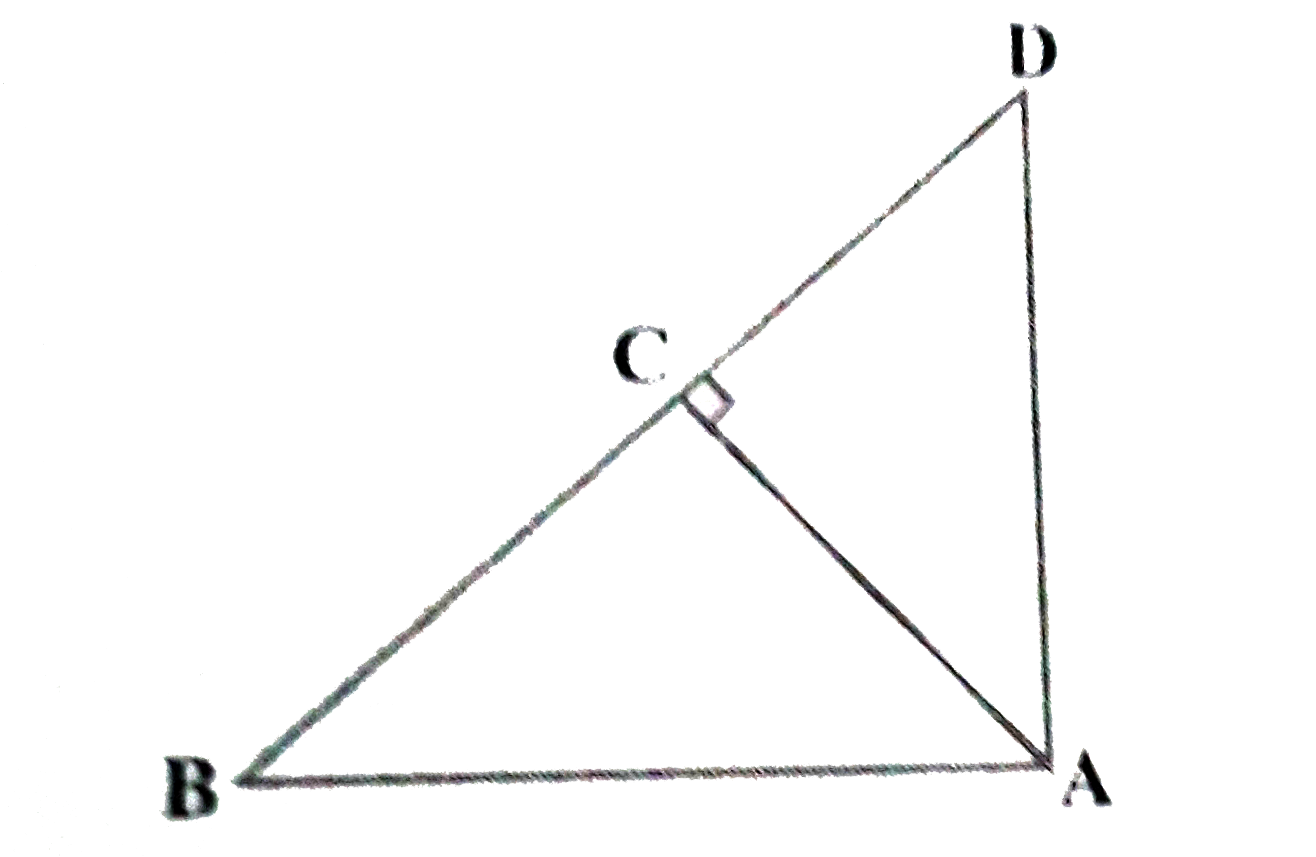
In Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
 View Solution
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View Solution(a+b+c−d)2−(a−b−c+d)2 =?
View Solution


