In a rectangle ABCD, AB=20cm, ∠BAC=60o , calculate side BC and diagonals AC and BD .
To solve the problem step by step, we will calculate the side BC and the diagonals AC and BD of rectangle ABCD, given that AB = 20 cm and angle BAC = 60°.
Step 1: Understand the Rectangle
We have a rectangle ABCD where:
- AB = 20 cm
- Angle BAC = 60°
Step 2: Identify the Sides
In rectangle ABCD:
- AB is one of the sides (20 cm).
- BC is the side opposite to AD.
- AC is the diagonal from A to C.
- BD is the diagonal from B to D.
Step 3: Calculate Side BC
Using the trigonometric ratio for angle A (which is 60°):
- We know that:
tan(A)=OppositeAdjacent=BCAB
- Substituting the known values:
tan(60°)=BC20
- The value of tan(60°) is √3:
√3=BC20
- Now, solving for BC:
BC=20⋅√3cm
Step 4: Calculate Diagonal AC
Using the cosine ratio for angle A (60°):
- We know that:
cos(A)=AdjacentHypotenuse=ABAC
- Substituting the known values:
cos(60°)=20AC
- The value of cos(60°) is 12:
12=20AC
- Now, solving for AC:
AC=20⋅2=40cm
Step 5: Calculate Diagonal BD
In a rectangle, the diagonals are equal:
- Therefore, BD=AC:
BD=40cm
Final Results
- Side BC = 20√3 cm
- Diagonal AC = 40 cm
- Diagonal BD = 40 cm
We have a rectangle ABCD where:
- AB = 20 cm
- Angle BAC = 60°
In rectangle ABCD:
- AB is one of the sides (20 cm).
- BC is the side opposite to AD.
- AC is the diagonal from A to C.
- BD is the diagonal from B to D.
Using the trigonometric ratio for angle A (which is 60°):
- We know that:
tan(A)=OppositeAdjacent=BCAB
- Substituting the known values:
tan(60°)=BC20
- The value of tan(60°) is √3:
√3=BC20
- Now, solving for BC:
BC=20⋅√3cm
Using the cosine ratio for angle A (60°):
- We know that:
cos(A)=AdjacentHypotenuse=ABAC
- Substituting the known values:
cos(60°)=20AC
- The value of cos(60°) is 12:
12=20AC
- Now, solving for AC:
AC=20⋅2=40cm
In a rectangle, the diagonals are equal:
- Therefore, BD=AC:
BD=40cm
- Side BC = 20√3 cm
- Diagonal AC = 40 cm
- Diagonal BD = 40 cm
Topper's Solved these Questions
Similar Questions
A paper is in the form of a rectangle ABCD in which AB=20 cm and BC=14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining part.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionIf ABCD is a rectangle with ∠BAC=32∘, find the measure of ∠DBC
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AB=10cm , AC=14cm and BC=6cm , find BD and DC (ii) If AC=4.2cm , DC=6cm and BC=10cm , find AB . (iii) If AB=5.6cm , AC=6cm and DC=3cm , find BC .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AD=5.6cm , BC=6cm and BD=3.2cm , find AC . (ii) If AB=10cm , AC=6cm and BC=12cm , find BD and DC .
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
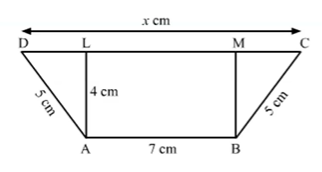
View Solution
