Define a triangle.
In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180∘. This property is called angle sum property of triangle.
If ABC is a triangle, then it is denoted as △ABC, where A, B and C are the vertices of the triangle. A triangle is a two-dimensional shape, in Euclidean geometry, which is seen as three non-collinear points in a unique plane.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
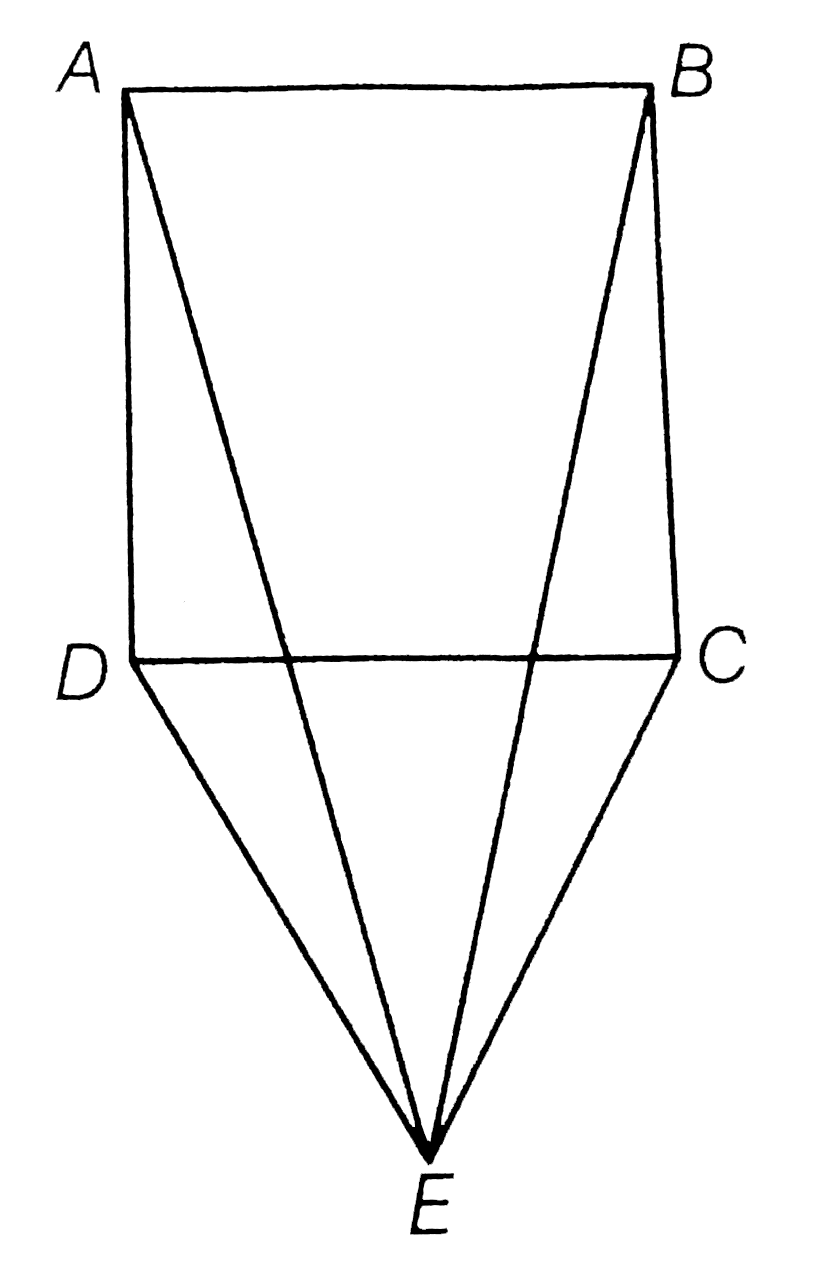 ARHSBSSSCAASDSAS
ARHSBSSSCAASDSASIf circumcentre lies in the exterior of the triangle then that triangle is ...... Triangle.
Aa right angledBan acute angledCan isocelesDan obtuse angledIf the circumcentre of a triangle lies outside it, then the triangle is
AEquilateralBAcute angledCRight angledDObtuse angled
Explain the following terms: Triangle (ii) parts or elements of a triangle Scalene triangle (iv) isosceles triangle Equilateral triangle (vi) acute triangle Right triangle (viii) obtuse triangle Interior of a triangle (x) exterior of a triangle.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle;then the triangle is isosceles.
View SolutionTwo sides of a triangle are in the ratio 3:5 and third side is 16 .If Δ is the largest possible area of the triangle,then Δ=
View SolutionConsider the following statements :
1. The orthocentre of a triangle always lies inside the triangle.
2. The centroid of a triangle always lies inside the triangle.
3. The orthocentre of a right angled triangle lies on the triangle.
4.The centroid of a right angled triangle lies on the triangle.
Which of the above statements are correct ?
View SolutionIf Δ1 is the area of the triangle formed by the centroid and two vertices of a triangle Δ2 is the area of the triangle formed by the mid- point of the sides of the same triangle, then Δ1:Δ2=
View Solution
