Question

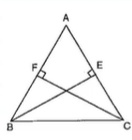
$ABC$
is a triangle is which $BE$
and $CF$
are, respectively, the perpendiculars to the sides
$AC$
and $AB$
. If $BE=CF$
, prove that $ABC$
is isosceles.

Explanation

"Given that ABC is a triangle in which BE and CF are perpendiculars to the sides AC and AB respectively such that BE=CF.
We have to prove that `triangle ABC` is an isosceles.
Now consider `triangle BCF and triangle CBE `, We have
`angle BCF = angle CEB = 90^@` ( given )
`BC=CB` (common sides )
`CF=BE` ( given )
`therefore triangle BFC= triangle CEB`
`angle FBC = angle ECB`
`angle ABC = angle ACB`
`AB = AC ` [ sides opposite to equal angles are equal ]
`therefore triangle ABC` is an isosceles .
"