In perpendiculars from
any point within an angle on its arms are congruent, prove that it lies on
the bisector of that angle.
Video Solution
Text Solution
Let P be a point within ∠ABC such that PM = PN. We have to provethatP lies on the bisector of ∠ABC i.e.,∠1=∠2.
In△sPMBandPNB
PM=PN ( given )
BP=BP ( common )
∠PNB=∠PMB ( right angle )
Therefore,△PMB=△PNB
∠1=∠2 [ ∴ angle B = angle C ]
Hence, P lies on the bisector of angle ABC.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentre - Question 2 - Select One
The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcenter
Two acute angles are congruent
View SolutionCongruent angles
View SolutionProve that, angles inscribed in the same are arc congruent.
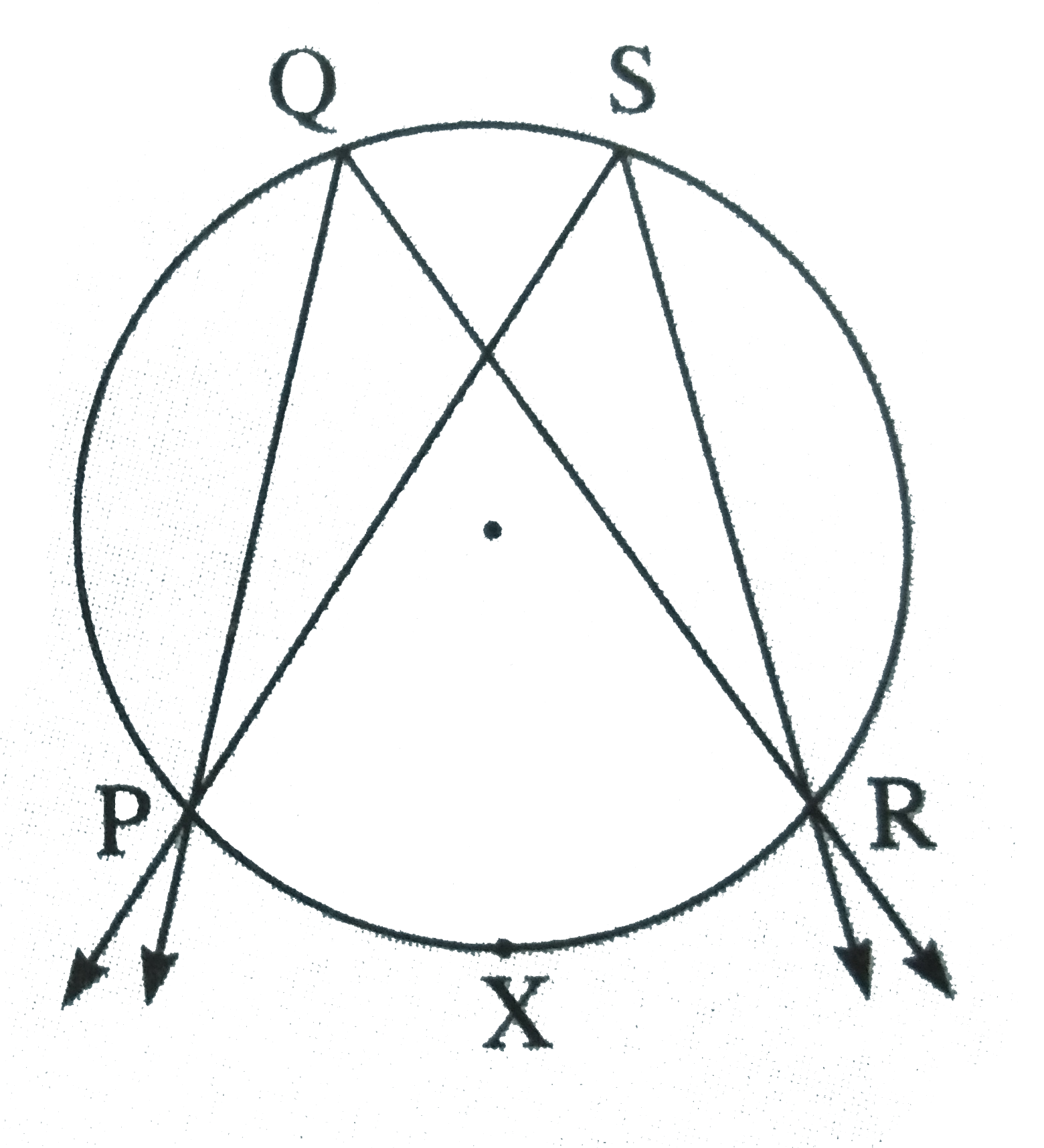 View Solution
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
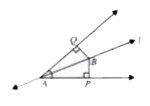
BP=BQ or B is equidistant from the arms of ∠A.View SolutionProve that median from the vertex of an isosceles Triangle is the bisector of the vertical angle
View SolutionProve that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
View Solution

