ABCD is a square, X and Y are points on sides AD and BC respectively such that AY=BX . Prove that BY=AX and ∠BAY=∠ABX
To prove that BY=AX and ∠BAY=∠ABX, we will use the properties of congruent triangles.
1. Identify the Given Information:
- Let ABCD be a square.
- Points X and Y are on sides AD and BC respectively.
- It is given that AY=BX.
2. Draw the Diagram:
- Draw square ABCD with points A,B,C,D.
- Mark points X on AD and Y on BC.
3. Label the Angles:
- Since ABCD is a square, ∠DAB=90∘ and ∠ABC=90∘.
4. Consider Triangles:
- We will consider triangles △ABX and △BAY.
5. Identify the Sides and Angles:
- In △ABX:
- AB is a side of the square.
- AX is the segment from A to X.
- BX is the segment from B to X.
- In △BAY:
- AB is the same side of the square.
- AY is the segment from A to Y (given AY=BX).
- BY is the segment from B to Y.
6. Establish Congruence:
- We have:
- ∠BAX=∠ABY=90∘ (both angles are right angles).
- AB=AB (common side).
- AY=BX (given).
- Therefore, by the RHS (Right angle-Hypotenuse-Side) criterion, triangles △ABX and △BAY are congruent.
7. Apply CPCTC:
- Since △ABX≅△BAY, by CPCTC (Corresponding Parts of Congruent Triangles are Congruent):
- BY=AX
- ∠BAY=∠ABX
8. Conclusion:
- We have proved that BY=AX and ∠BAY=∠ABX.
- Let ABCD be a square.
- Points X and Y are on sides AD and BC respectively.
- It is given that AY=BX.
- Draw square ABCD with points A,B,C,D.
- Mark points X on AD and Y on BC.
- Since ABCD is a square, ∠DAB=90∘ and ∠ABC=90∘.
- We will consider triangles △ABX and △BAY.
- In △ABX:
- AB is a side of the square.
- AX is the segment from A to X.
- BX is the segment from B to X.
- In △BAY:
- AB is the same side of the square.
- AY is the segment from A to Y (given AY=BX).
- BY is the segment from B to Y.
- We have:
- ∠BAX=∠ABY=90∘ (both angles are right angles).
- AB=AB (common side).
- AY=BX (given).
- Therefore, by the RHS (Right angle-Hypotenuse-Side) criterion, triangles △ABX and △BAY are congruent.
- Since △ABX≅△BAY, by CPCTC (Corresponding Parts of Congruent Triangles are Congruent):
- BY=AX
- ∠BAY=∠ABX
- We have proved that BY=AX and ∠BAY=∠ABX.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
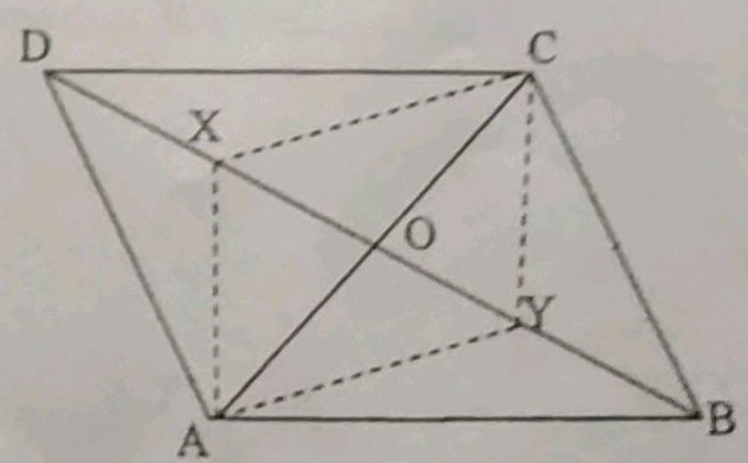 View Solution
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
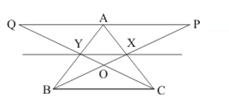 View Solution
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
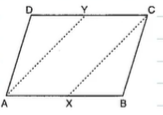 View Solution
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View Solution

