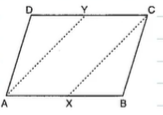
ABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD) GIVEN : A parallelogram ABCD in which X and Y are the mid-points of BC and CD respectively. TO PROVE : ar(AXY)=38ar(∣∣gmabcd) CONSTRUCTION : Join BD.
In∠BCD
X and Y are midpoint of sides BC and CD
XY||BD and XY=1/2BD
ar(∠CXY)=14⋅ar(∠ABC)
ar(∠CYX)=18⋅ar(parallelogramABCD)−(1)
ParallelogramABCD and ∠ABX
AD||BX
BX=12BC
∠ABX=14(∣∣gramABCD)−(2)
ar(∠AYD)=14ar(∣∣gramABCD)−(3)
ar(∣∣gramABCD)=ar(∠ABX)+ar(∠AYB)+ar(CYX)+ar(∠AXY)
ar(AXY)=ar(∣∣gramABCD)−[ar(∠ABX)+ar(∠ATD)+ar(∠CYX)]
ar(∠AXY)=(1−58)ar(∣∣gramABCD)
ar(∠AXY)=38ar(∣∣gramABCD).
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionShow that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms. GIVEN : A parallelogram ABCD.E and F are the mid-points of opposite sides AB and CD respectively. TO PROVE : ar(^(gm)AEFD)=ar(^(gm)EBCF) CONSTRCUTION : Join EF.
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View Solution
