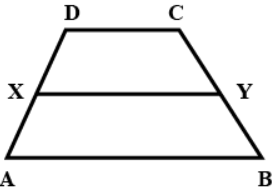
In Figure, ABCD
is a trapezium in which ABDC
and DC=40cm
and AB=60cm.
If X
and Y
are, respectively, the mid-points of AD
and BC
, prove that :
XY=50cm
DCYX
is a
trapezium
ar(trap.DCYX)=911ar(trap.XYBA
Step by step video & image solution for In Figure, A B C D is a trapezium in which A B D C and D C=40c m and A B=60c mdot If X and Y are, respectively, the mid-points of A D and B C , prove that : X Y=50c m D C Y X is a trapezium a r(t r a pdotD C Y X)=9/(11)a r(t r a pdot(X Y B A) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a trapezium in which AB,DCandDC=40cmandAB=60cm If XandY are, respectively, the mid-points of ADandBC, prove that: ar(traptDCYX)=911,ar(trap(XYBA)
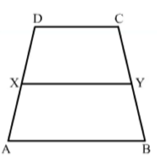
View SolutionIn Figure, ABCD is a trapezium. Find the value of x and y
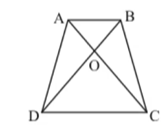
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
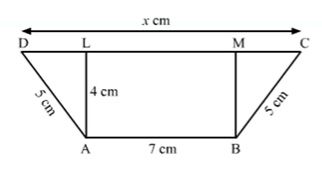
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
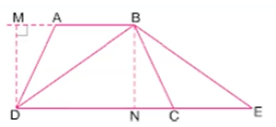
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View Solution
