In Figure, ABCD is a rectangle with sides AB=10cm and AD=5cm. Find the area of EFG
Step by step video & image solution for In Figure, A B C D is a rectangle with sides A B=10 c m\ a n d\ A D=5c mdot Find the area of E F G by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a rectangle in which CD=6cm,AD=8cm Find the area of parallelogram CDEF

View SolutionIn Fig. 32, ABCD is a rectangle of length AB=40 cm and breadth BC=25 cm. If P,Q,R,S be the mid-points of the sides AB, BC, CD and DA respectively, find the area of the shaded region.
View SolutionIn Fig.38, ABCD and PQRC are square such that AD=22 cm and PC=y cm. If the area of the shaded region is 403 cm2, then the value of y is (a)3 (b) 6 (c)9 (d) 10
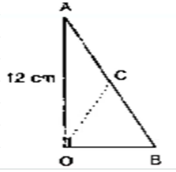
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionIn Fig. 15.93, ABCD is a rectangle with AB=14 cm and BC=7 cm . Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region. (FIGURE)
View SolutionIn Fig 31, ABCD is a rectangle with dimensions 32 m by 18 m. ADE is a triangle such that EF⊥AD and EF=14 cm. Calculate the area of the shaded region.
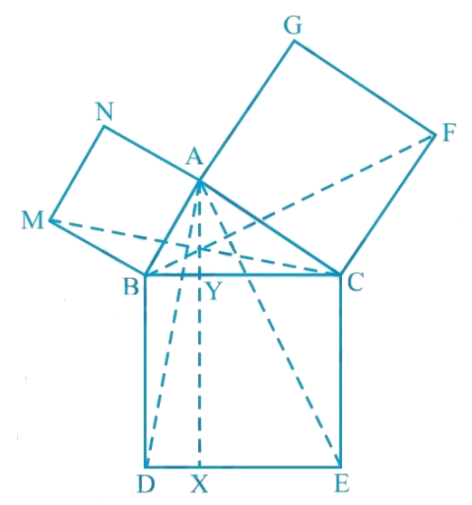
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
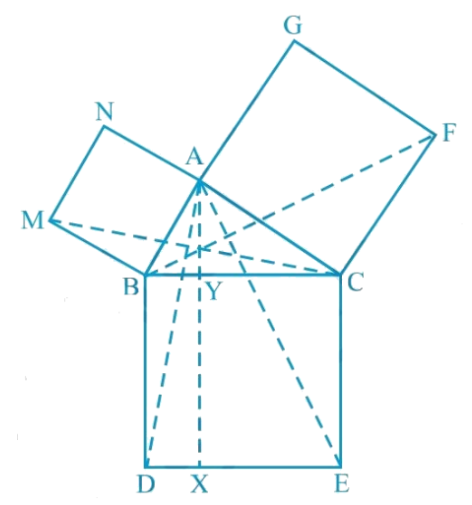
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
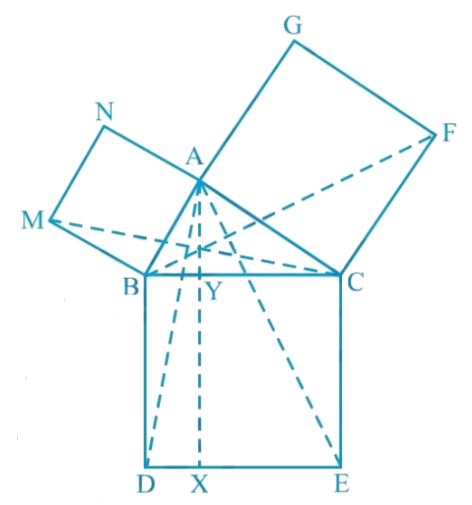
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
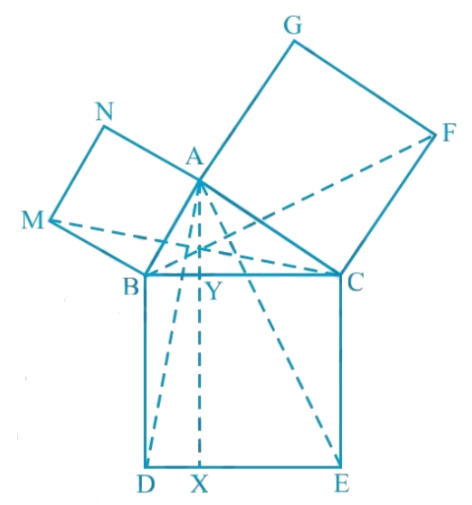
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN)
View Solution
