Two circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
JoinAC,AD,BC,BDandAB
In △ACBand△ADB
AC=AD(Radii of the same circle)
BC=BD(Radii of the same circle)
AB=AB(Common Circle)
△ACB=△ADB (By SSS)
∠ACB=∠ADB
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D. then.
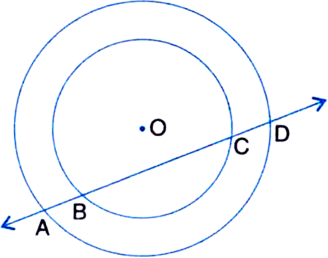 AAB=BDBCD=ACCAB=CDDNone
AAB=BDBCD=ACCAB=CDDNone
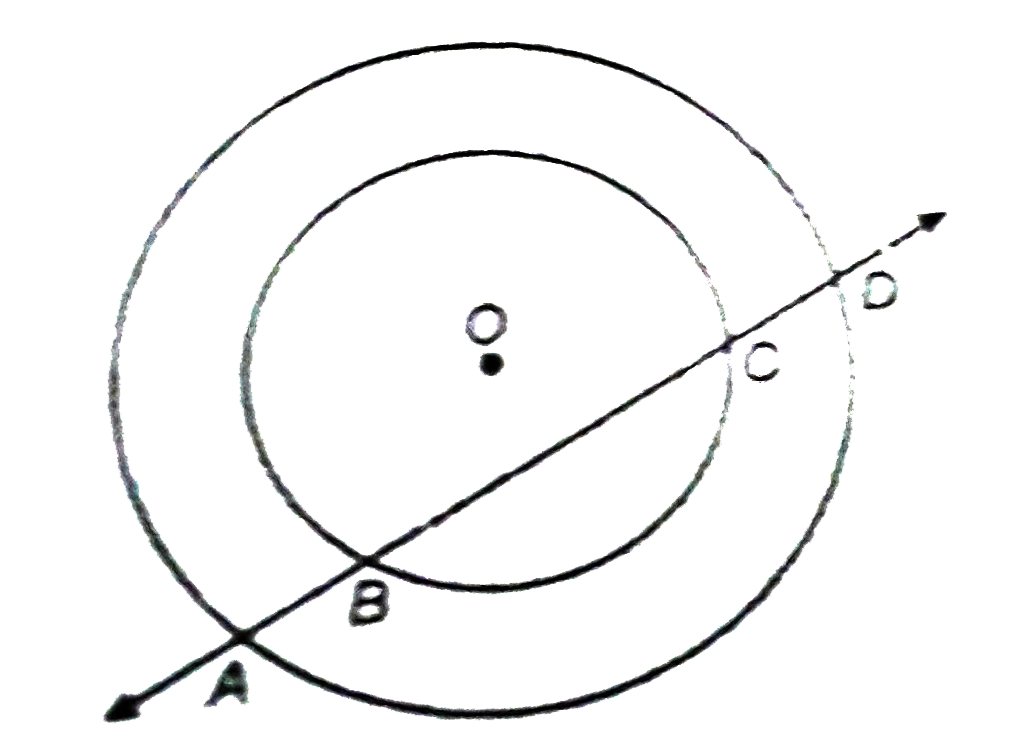
If a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
 View Solution
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionIf the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C+∠D=k∠AOB, then find the value of k
View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
View Solution

