In ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC). TO PROVE : ar(BPQ)=12ar(ABC) CONSTRUCTION : Join CD.
To prove that the area of triangle BPQ is equal to half the area of triangle ABC, we will follow these steps:
1. Identify the Midpoints:
- Given triangle ABC, point D is the midpoint of side AB. This means AD=DB.
2. Construct Line Segment:
- Join point C to point D to form segment CD.
3. Understand the Properties of the Median:
- Since D is the midpoint of AB, segment CD is a median of triangle ABC. A median divides the triangle into two smaller triangles of equal area. Therefore, the area of triangle BDC is equal to half the area of triangle ABC:
Area(BDC)=12Area(ABC)
4. Identify the Parallel Lines:
- Point P is defined as the midpoint of segment CD. The line segment CQ is drawn parallel to DP.
5. Use the Property of Triangles on Parallel Lines:
- Triangles PDQ and PDC share the same base DP and are between the same parallel lines DP and CQ. Therefore, the areas of these triangles are equal:
Area(PDQ)=Area(PDC)
6. Express Area of Triangle BDC:
- The area of triangle BDC can be expressed as the sum of the areas of triangles BDP and PDC:
Area(BDC)=Area(BDP)+Area(PDC)
7. Substitute Known Areas:
- From step 3, we know that:
Area(BDC)=12Area(ABC)
- Substituting Area(PDC) with Area(PDQ) (from step 5):
Area(BDC)=Area(BDP)+Area(PDQ)
8. Combine the Equations:
- Now we can write:
12Area(ABC)=Area(BDP)+Area(PDQ)
9. Express Area of Triangle BPQ:
- Since BPQ is formed by combining BDP and PDQ, we can conclude:
Area(BPQ)=Area(BDP)+Area(PDQ)
10. Final Conclusion:
- Therefore, we have:
Area(BPQ)=12Area(ABC)
- This completes the proof.
- Given triangle ABC, point D is the midpoint of side AB. This means AD=DB.
- Join point C to point D to form segment CD.
- Since D is the midpoint of AB, segment CD is a median of triangle ABC. A median divides the triangle into two smaller triangles of equal area. Therefore, the area of triangle BDC is equal to half the area of triangle ABC:
Area(BDC)=12Area(ABC)
- Point P is defined as the midpoint of segment CD. The line segment CQ is drawn parallel to DP.
- Triangles PDQ and PDC share the same base DP and are between the same parallel lines DP and CQ. Therefore, the areas of these triangles are equal:
Area(PDQ)=Area(PDC)
- The area of triangle BDC can be expressed as the sum of the areas of triangles BDP and PDC:
Area(BDC)=Area(BDP)+Area(PDC)
- From step 3, we know that:
Area(BDC)=12Area(ABC)
- Substituting Area(PDC) with Area(PDQ) (from step 5):
Area(BDC)=Area(BDP)+Area(PDQ)
- Now we can write:
12Area(ABC)=Area(BDP)+Area(PDQ)
- Since BPQ is formed by combining BDP and PDQ, we can conclude:
Area(BPQ)=Area(BDP)+Area(PDQ)
- Therefore, we have:
Area(BPQ)=12Area(ABC)
- This completes the proof.
Topper's Solved these Questions
Similar Questions
In A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
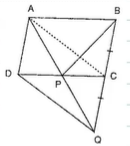
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
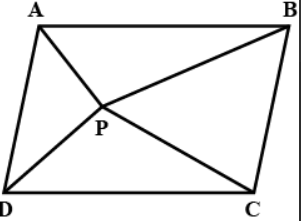
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
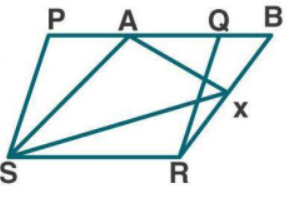
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
View Solution
