In Figure, O is the centre of the circle and ∠DAB=500. Calculate the values of x and y
Video Solution
Text Solution
It is given that O is the centre of the circle
∠DAB=500
We know that the radii of the circle are equal
OA=OB
∠OAB+∠OBA+∠AOB=1800
500+500+∠AOB=1800
∠AOB=800
x=1800−800=1000
We know that the opposite angles of a cyclic quadrilateral are supplementary
∠DAB+∠BCD=1800
500+∠BCD=1800
∠BCD=1800−500=1300=y
Therefore the value of xis 1000and yis1300
.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the following figure, O is the centre of the circle and ∠PRQ=50∘. What is the value (in degrees) of ∠PTQ?
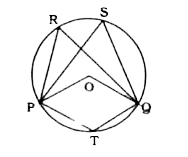 A100B75C130D150
A100B75C130D150 - Question 2 - Select One
In the adjoining figure, O is the centre of circle. If ∠DAB=50∘ find the values of x and y.
 Ax=110∘,y=70∘Bx=90∘,y=90∘Cx=100∘,y=80∘Dx=130∘,y=50∘
Ax=110∘,y=70∘Bx=90∘,y=90∘Cx=100∘,y=80∘Dx=130∘,y=50∘
In the figure, O is the centre of the circle. If ∠ADC=140∘, then what is the value of x?
View SolutionIn figure, O is the centre of the circle ∠BCO=30∘ . Find X and Y.
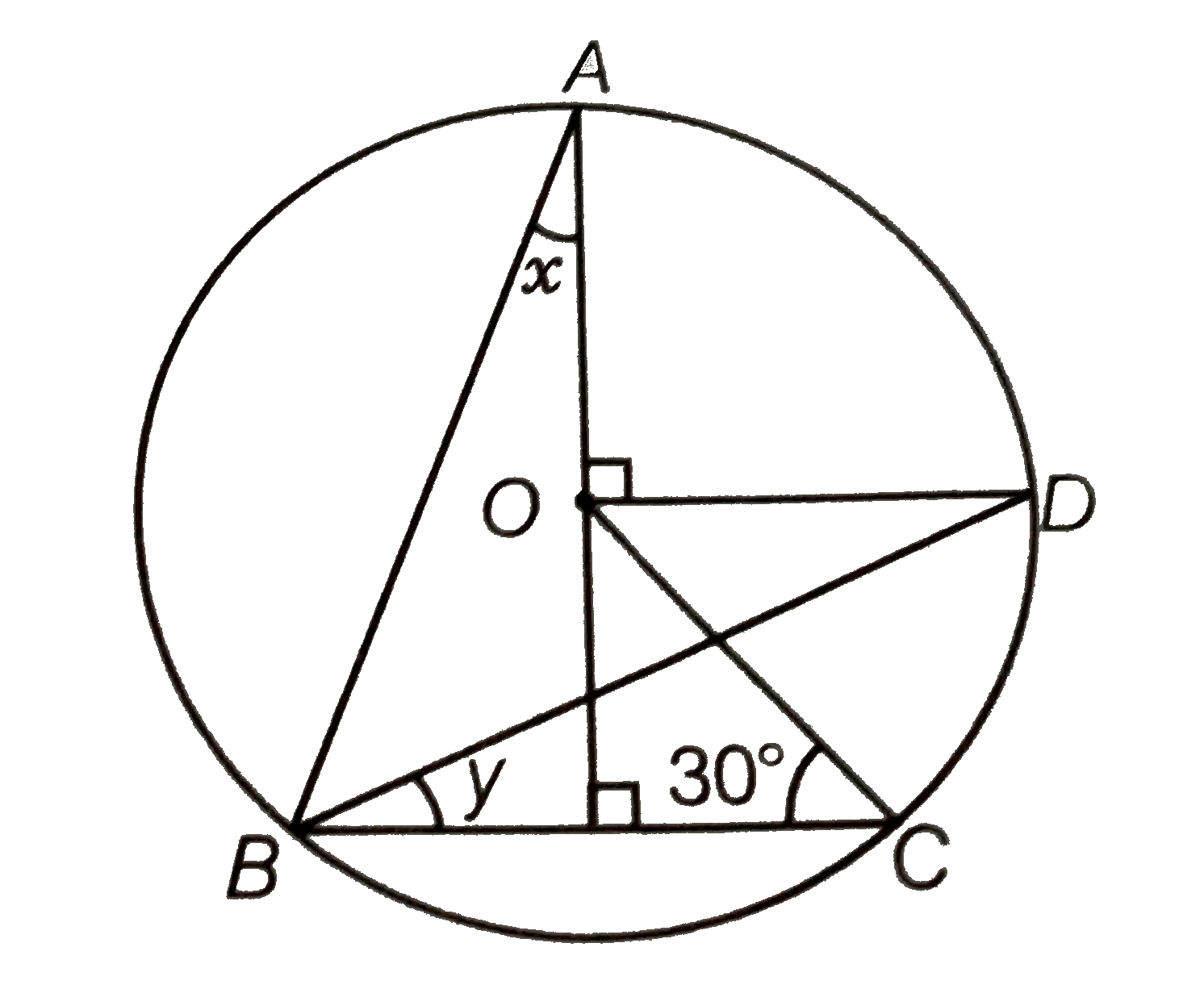 View Solution
View SolutionIn Figure, O is the centre of the circle. If ∠CEA=300, find the values of x, y and z
View SolutionIn Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View SolutionIn the following figure O is the centre of circle and ∠ACB=x0,∠OBA=y0 then the value of x0+y0 is
View Solution

