A glass hemisphere of radius 0.04 m and refractive index of the material 1.6 is placed centrally over cross mark on a paper (i) with the flat face, (ii) with the curved face in contact with the paper. In each case, the cross mark is viewed directly from above. The position of the images will be
(i) 0.04 m from the flat face, (ii) 0.025 m from the flat face
(i) at the same position of the cross mark, (ii) 0.025 m below the flat face
(i) 0.025 m from the flat face, (ii) 0.04 m from the flat face
for both (i) and (ii) 0.025 m from the highest point of the hemisphere
The correct Answer is:B

μ2v−μ1u=μ2−μ1R
1v−1.6−0.04=1−1.6−0.04
v=−0.04m
Image of O is formed O.
1v−1.6−0.04=0
v=−0.041.6=−0.025m
PI=0.025m

Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES67videos
REFLECTION OF LIGHT
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
Similar Questions
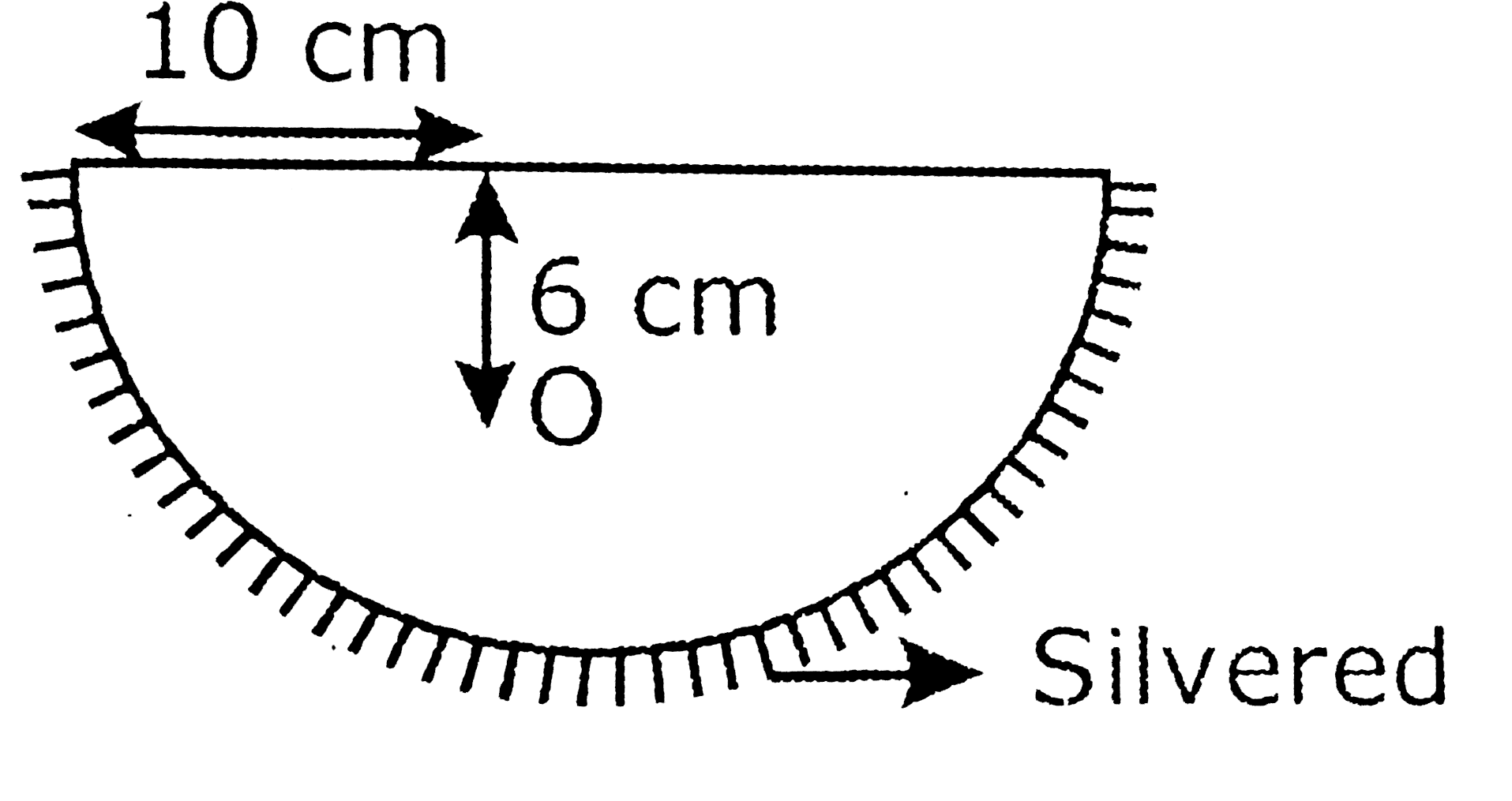
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View SolutionA hemisphere of radius R, made of glass of refractive index (3/2) is placed on 'the table. A point source of light is placed at a distance 2R from the centre, of hemisphere. If source is viewed diametrically opposite side of hemisphere. Find the position of image of source.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A glass slab of thickness 3cm and refractive index 3/2 is placed on ink mark on a piece of paper. For a person looking at the mark at a distance 5.0cm above it, the distance of the mark will appear to be
A3.0cmB4.0cmC4.5cmD5.0cm - Question 2 - Select One
A glass slab of thickness 3cm and refractive index 3/2 is placed on ink mark on a piece of paper. For a person looking at the mark at a distance 5.0cm above it, the distance of the mark will appear to be
A3.0cmB4.0cmC4.5cmD5.0cm - Question 3 - Select One
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.
 Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left side
Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left side
A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
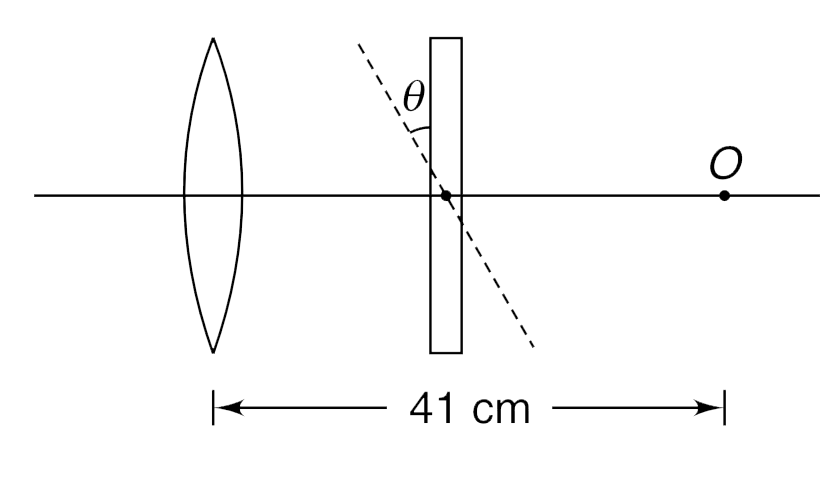
View SolutionA point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
 View Solution
View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the centre of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through centre.
View SolutionA cylinderical glass rod of radius 0.1m and refractive index √3 lies on a horizontal plane mirror. A horizontal ray of light moving perpendicular to the axis of the rod is incident on it. At what height from the mirror should the ray be incident so that it leaves the rod at a height of 0.1m above the plane mirror? At what centre to centre distance a second similar rod, parallel to the first, be placed on the mirror, such that the emergent ray from the second rod is in line with the incident ray on the first rod?
 View Solution
View SolutionFigure shows a point object placed in front of a transparent sphere of radius 20 cm and refractive index 1.5. The sphere forms an image due to refraction at surface I followed by refraction at surface II. The sphere is kept in air and the object is located at distance x from P1. It is found that for x>x1, the image formed due to refraction at surface I is real, the final image formed by the sphere is also real and forms to the right of P2. For x2<x<x1, the image formed by surface I is virtual while the final image formed by the sphere is real and forms to the right of P2. However for x<x2, the image formed by surface I and also the final image formed by the sphere are virtual. It is also found that the final image is virtual if the distance of image formed by surface I from P2 is less than y. The object is now moved away from the sphere so that x becomes large and say, x→∞. In the given sphere is replaced by another one of the same radius but of refractive index 2.5, the final image is formed at distance y2 from P2.
As stated above, if the distance of image formed by Surface 1 from P2 is less than y, the final image is virtual. Then, y will be
 View Solution
View Solution

