A thin rod of mass M and length L is bent in a semicircle as shown in figure (a). What is its gravitational force (both magnitude and direction) on a particle with mass m at O the centre of curvature ? (b) what would be the force on m if the rod is in the form of complete circle?
_S01_007_S01.png)
(a). Considering an element of rod of length dl as shown in figure and treating it s a point of mass (M/L) dl situated at a distance R from P, the gravitational force due to this element o the particle will be
dF=Gm(M/L)(Rdthη)R2 along OP [as dl=Rdthη]
So the component of this force along x and y-axis will be ltbr dFx=dFcosθ=GmMcosθdθLR,dFy=dFsinθ=GmMsinθdθLR
So that Fx=GmMLR∫π0cosθdθ=GmMLR[sinθ]π0=0
and Fy=GmMLR∫π0sinθdθ=GmMLR[−cos]π0=2πGmML2[asR=Lπ]
So F=√F2x+F2y=Fy=2πGmML2 [as Fxis zero]
i.e., the resultant force is along the y-axis and has magnitude [2πGmM/L2]
(b). If the rod was bent into a complete circle,
Fx=GmMLR∫2π0cosθdθ=0 and also, Fy=GmMLR∫2π0sinθdθ=0
I.e., the resultant force on m at O due to the ring is zero.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)28videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)27videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
Similar Questions
A thin rod of mass M and length L is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass m at the centre of curvature?
View SolutionA rod of mass M and length L is bent to form a semicircle. The MOI about an axis perpendicular to plane of semicircle about its center is
View Solution
Knowledge Check
- Question 1 - Select One
A thin rod of length L is bent to form a semi circle. The mass of the rod is M. What will be the gravitational potential at the centre of the circle?
A−GMLB−GM2πLC−πGM2LD−πGML - Question 2 - Select One
A thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
A−GMLB−GM2πLC−πGM2LD−πGML - Question 3 - Select One
A thin rod of mass M and length L is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
AML22π2BML24π2CML28π2DML2π2
A rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
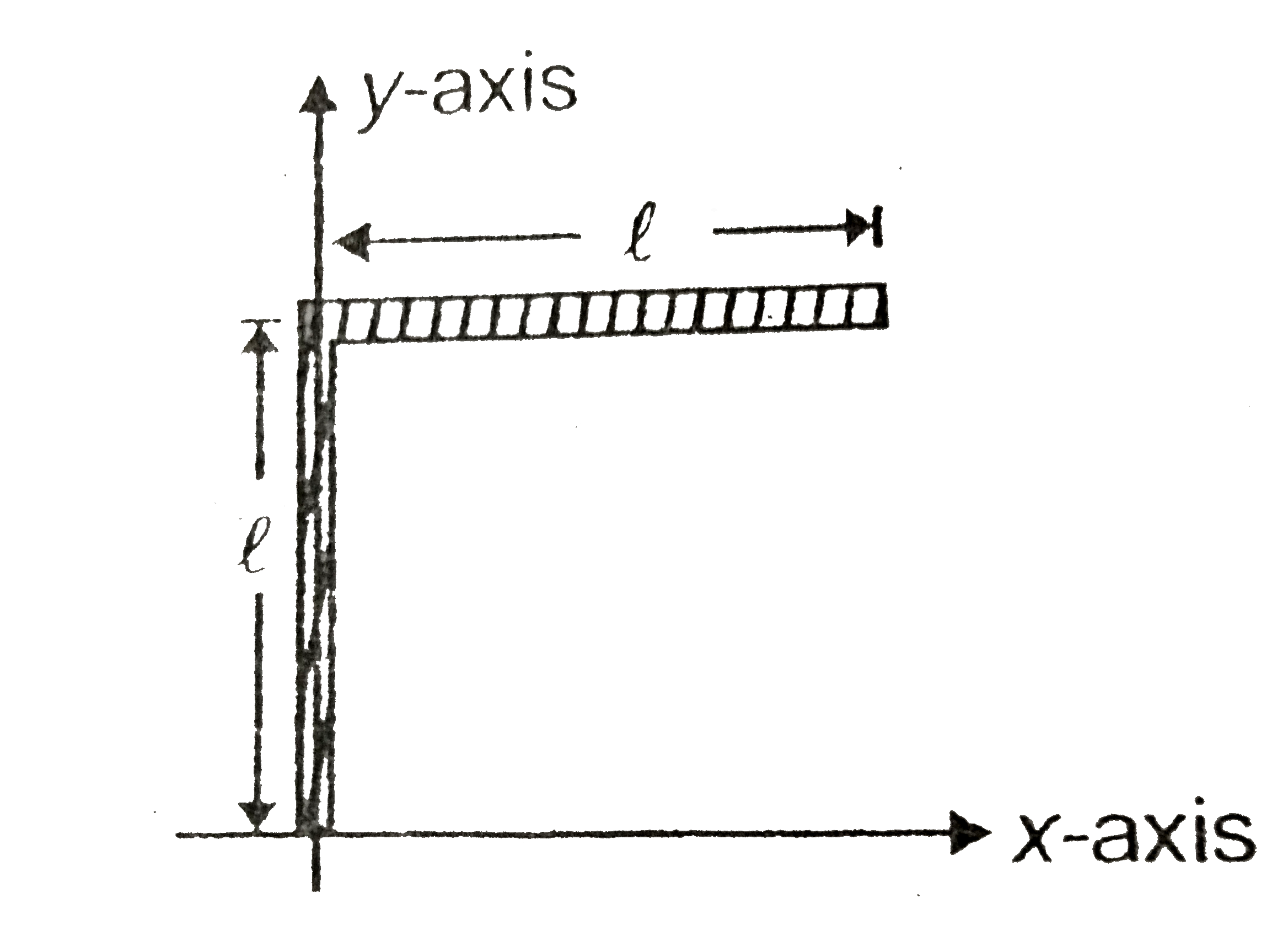 View Solution
View Solution" The force of attraction on a particle of mass "m" placed at the centre of curvature of a semicircular wire of length L and mass "M" is "
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 View Solution
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 View Solution
View SolutionA rod of lengthL and mass M0 is bent to form a semicircular ring as shown. The M.I. about X'X is
 View Solution
View Solution

