A thin rod of mass M and length L is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass m at the centre of curvature?
consider an elements of rod of length dl as shown in diagram and treat it as a small particle of mass (M/L)dl situated at a distance R from P. Then gravitational force due to the element on the particle will be
dF=Gm(M/L)(Rdθ)R2 along OP
[asdl=Rdθ]
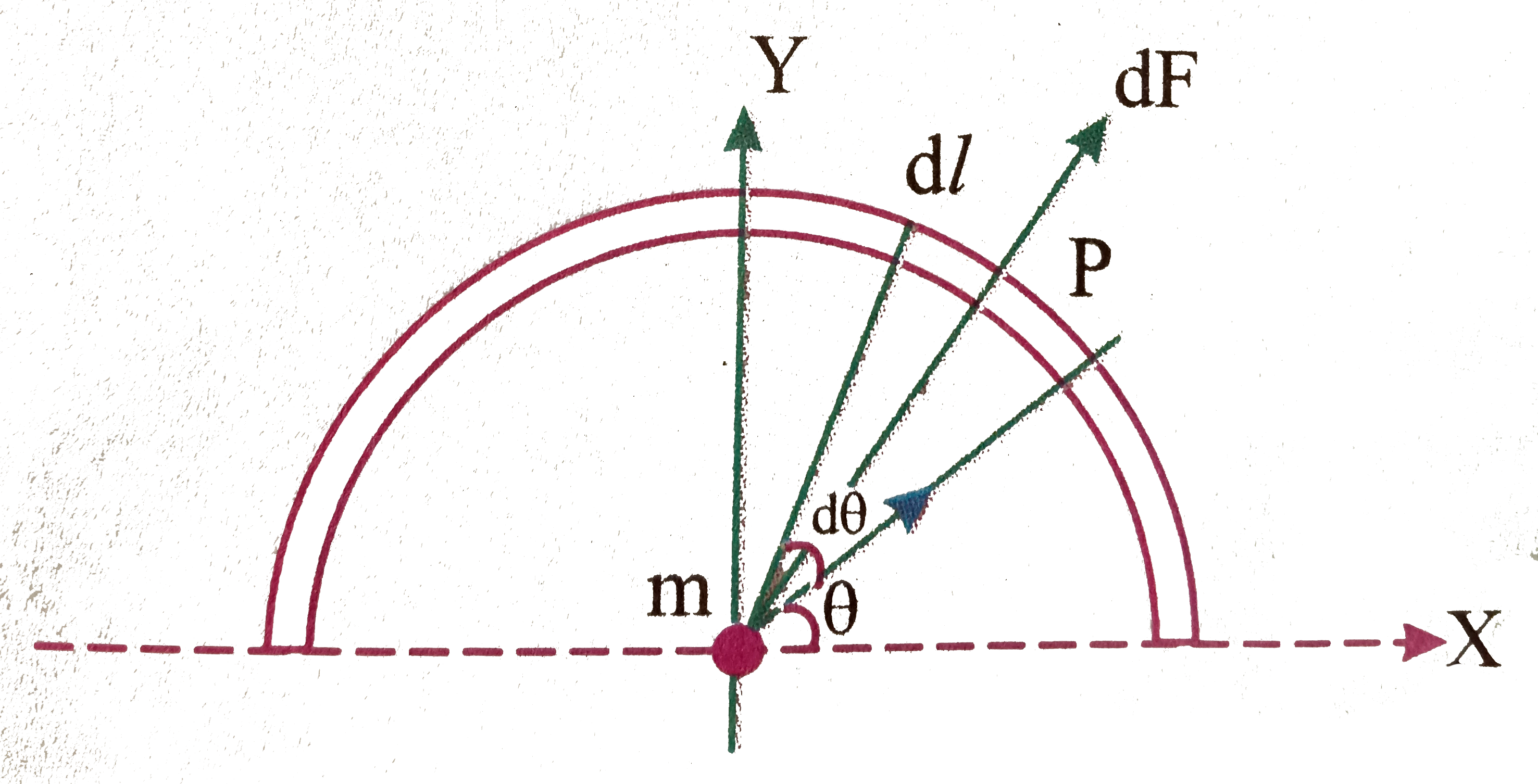
so the components of this force along X and Y axes will be
dFx=dFcosθ=GmMcosθdθLR
dFy=dFsinθ=GmMcosθdθLR
So that
Fx=GmMLR∫π0cosθdθ=GmMLR[sinθ]π0=0
Fy=GmMLR∫π0sinθdθ=GmMLR[−cosθ]π0
=2πGmML2 [asR=Lπ]
F=√F2x+F2y=Fy=2πGmML2 (asFx=0)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - C.U.Q220videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL I(C.W.)51videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
A thin rod of mass M and length L is bent in a semicircle as shown in figure (a). What is its gravitational force (both magnitude and direction) on a particle with mass m at O the centre of curvature ? (b) what would be the force on m if the rod is in the form of complete circle?
View SolutionConsider the situation as shown in the following diagrams. Find net gravitational force on the particle of mass m.
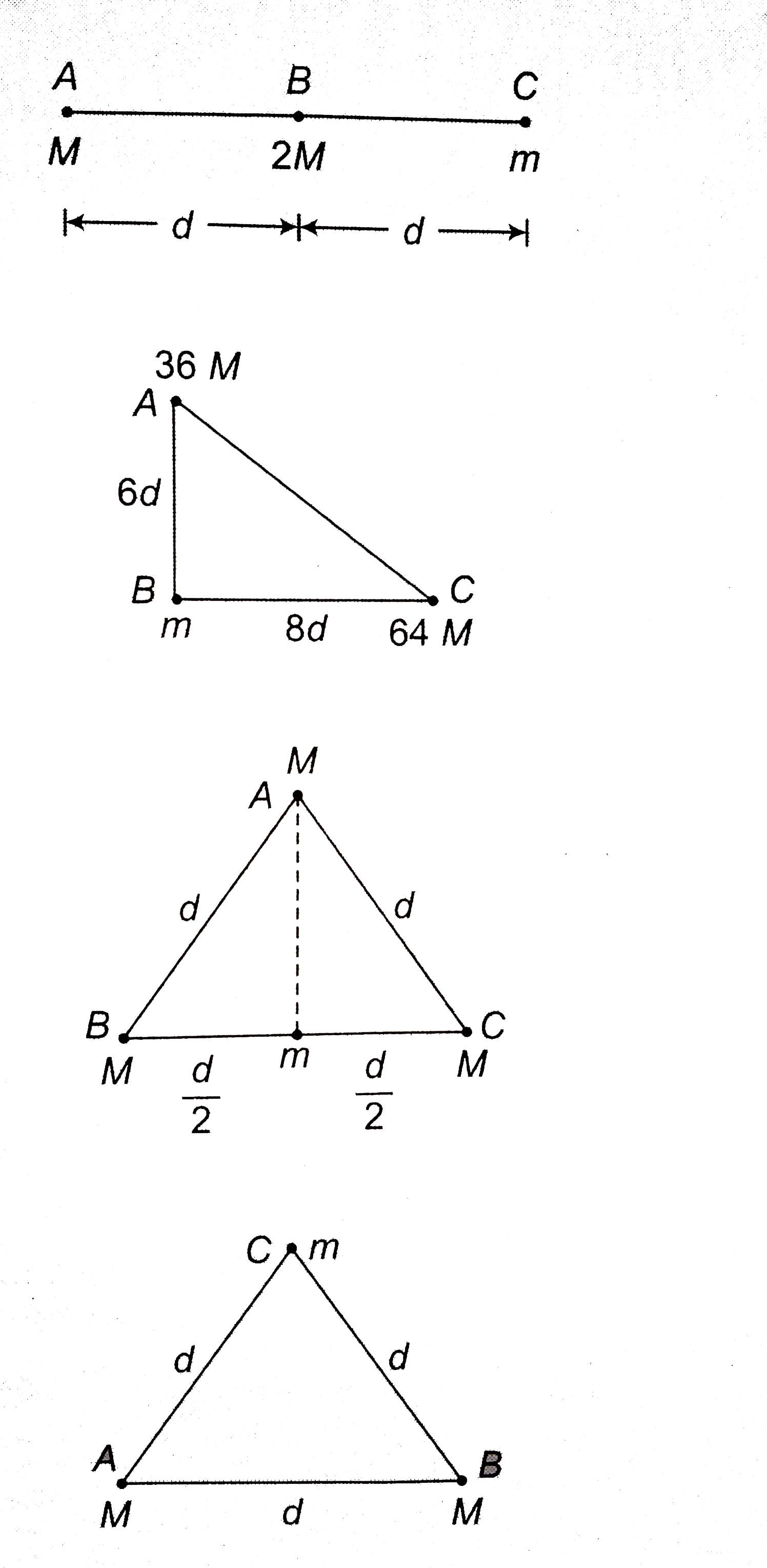
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
A−GMLB−GM2πLC−πGM2LD−πGML - Question 2 - Select One
A thin rod of length L is bent to form a semi circle. The mass of the rod is M. What will be the gravitational potential at the centre of the circle?
A−GMLB−GM2πLC−πGM2LD−πGML - Question 3 - Select One
A thin rod of mass M and length L is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
AML22π2BML24π2CML28π2DML2π2
Consider a uniform rod of mas M and length L. It is bent into a semicircle. Its moment of inertia about a line perpendicular to the plane wire passing through the centre is
View SolutionA rod of mass M and length L is bent to form a semicircle. The MOI about an axis perpendicular to plane of semicircle about its center is
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.
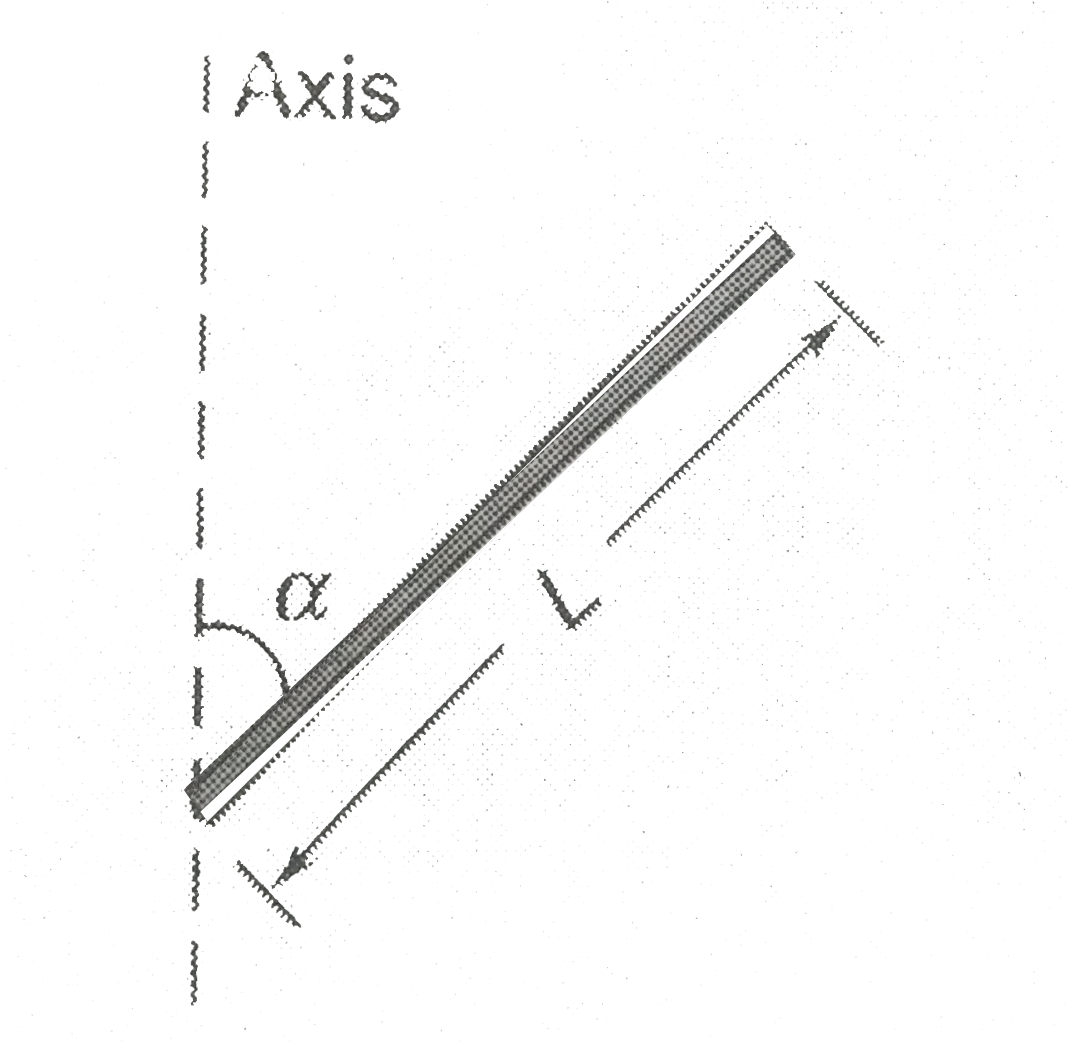 View Solution
View SolutionA rod of lengthL and mass M0 is bent to form a semicircular ring as shown. The M.I. about X'X is
 View Solution
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 View Solution
View Solution

