
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
3
2
√3
√2
The correct Answer is:A

Conservation of momentum of (M+m)
2mv0=Mv1 .(i)
Newton's second law:
v0cos30∘=v1cos30∘+v2cos60∘
√3v0=√3v1+v2 .(ii)
For 'm' v0sin30∘=v2sin60∘ ....(iii)
⇒v2=v0√3,v1=23v0
from (i) 2mv0M=2v03
(mM)=13⇒(Mm)=3
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution
Knowledge Check
- Question 1 - Select One
The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A12MR2B14MR2CMR2D34MR2 - Question 2 - Select One
Three identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
A2R3B2RC5R3D4R3 - Question 3 - Select One
The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
A12Mr2BMt2C25Mr2D14Mr2
Given a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
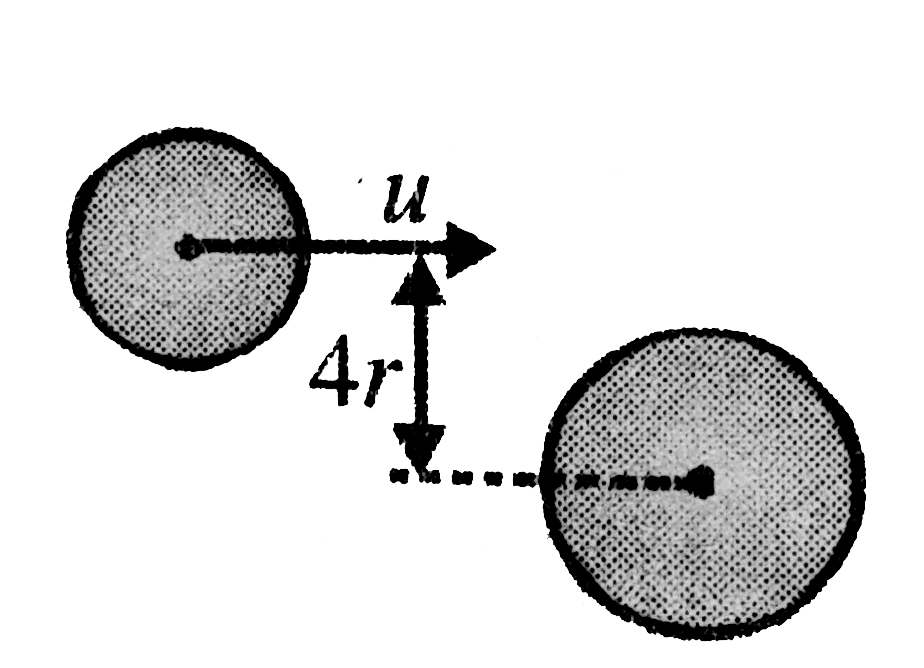 What is the final velocity of the heavier disc?View Solution
What is the final velocity of the heavier disc?View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
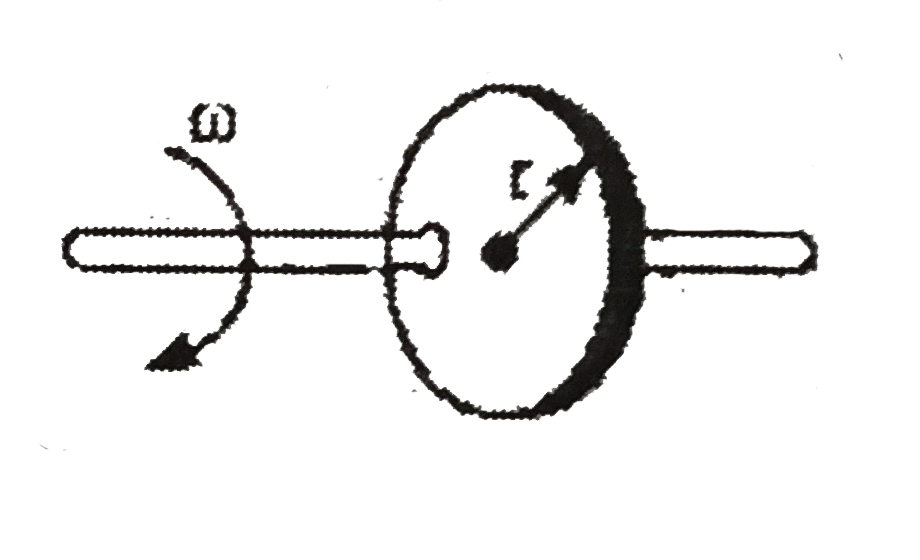 View Solution
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to the plane at an angular velocity ω . Another disc of mass M / 3 but same radius is placed gently on the first disc coaxially . the angular velocity of the system now is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View Solution

