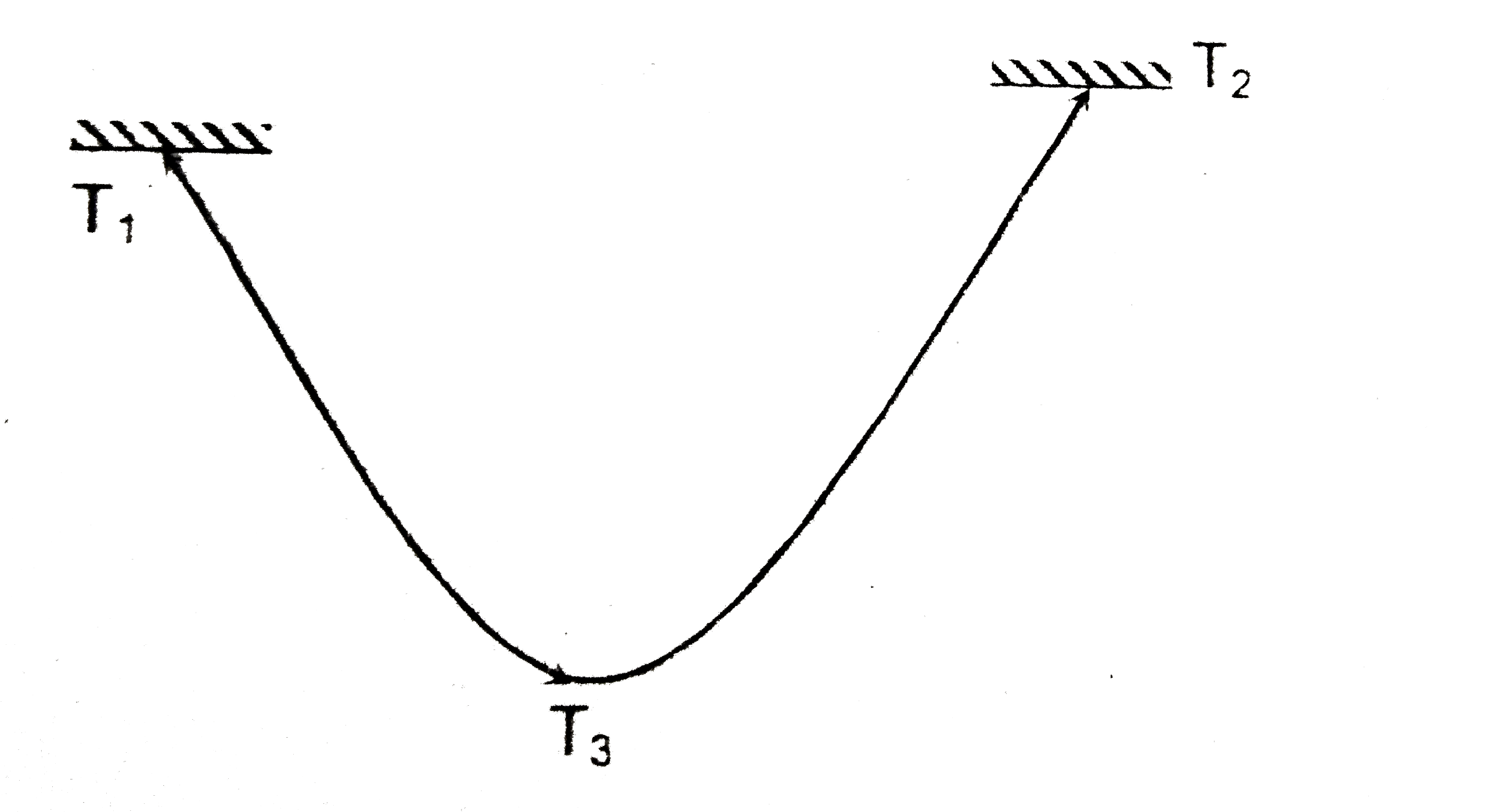
 ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
√T21−T23+√T22−T23g
(T1+T2−2T3)g
√T21+T22g
√T21+T23+√T22+T23g
The correct Answer is:A
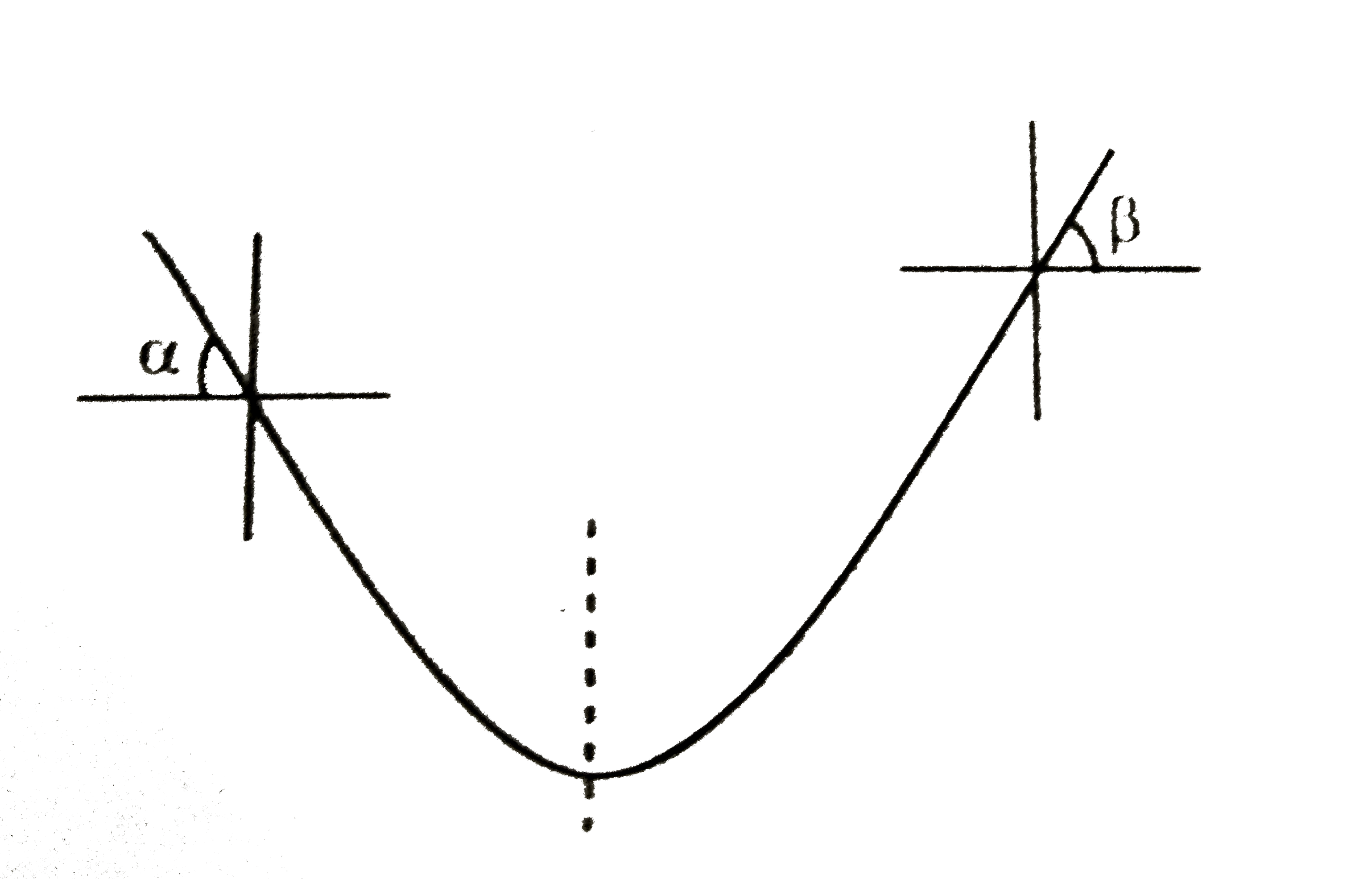
T1cosα=T3=T2cosβ
T1sinα+T2sinβ=mg
⇒mg=T1√1−(T3T1)2+T2√1−(T3T2)2
⇒m=√T21+T23+√T22−T23g
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml - Question 2 - Select One
In fig tension in the string that connects the masses A and B is T1 and that in the string connecting B and C is T2 then T1T2 is:
 A2B0.5C4D0.25
A2B0.5C4D0.25 - Question 3 - Select One
If the normals drawn at the points t1 and t2 on the parabola meet the parabola again at its point t3, then t1t2 equals.
A2B−1C−2Dt3−2t3
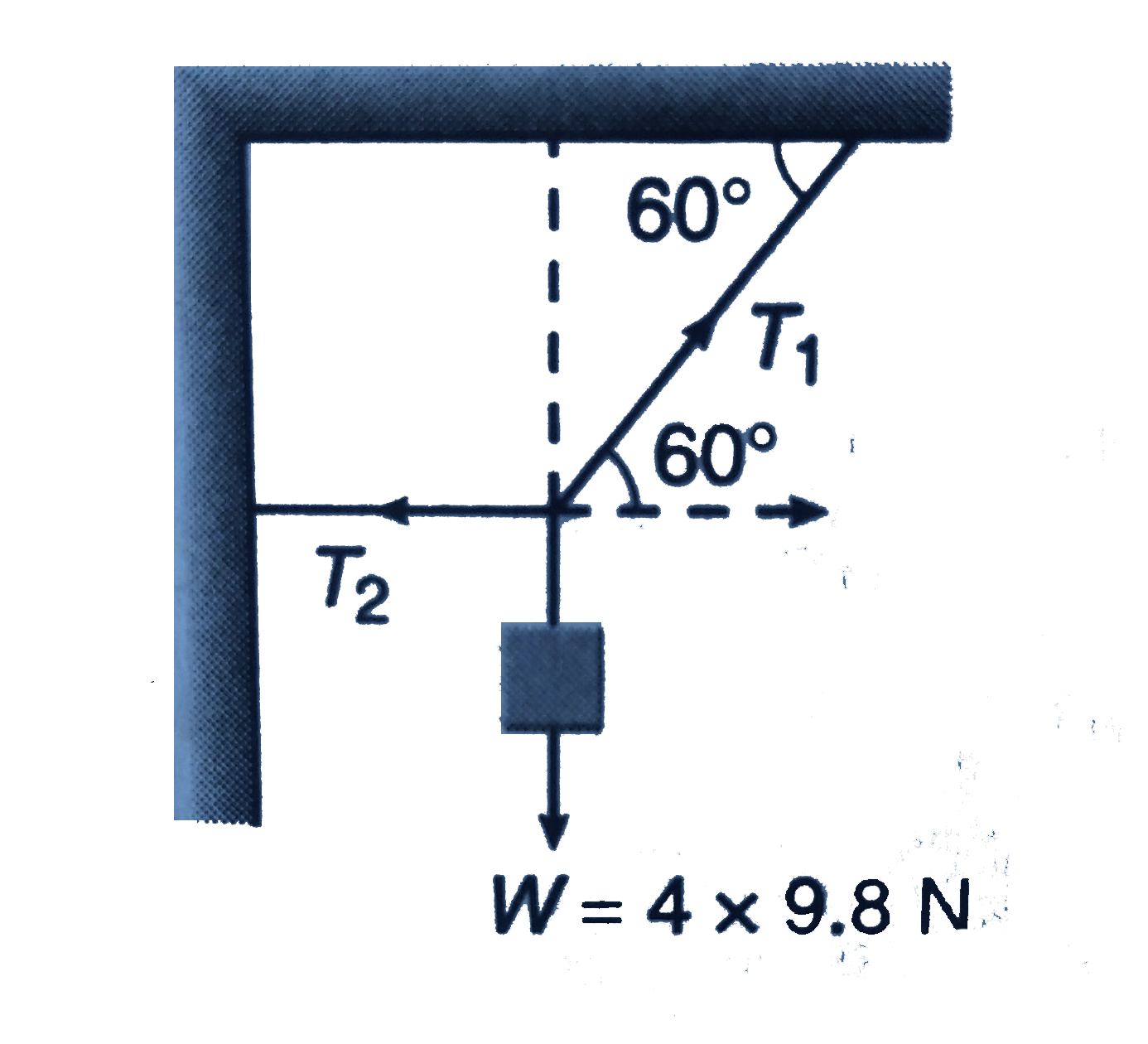
A block of mass 10 kg is suspended with two strings as shown in the fig. Find the tensions T1andT2 in the two string.
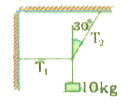 View Solution
View SolutionDetermine the tensions T1 and T2 in the strings as shown in figure.
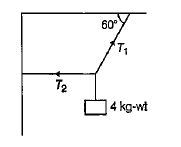 View Solution
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is
 View Solution
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tension T1 in the horizontal string (in kg wt ) is
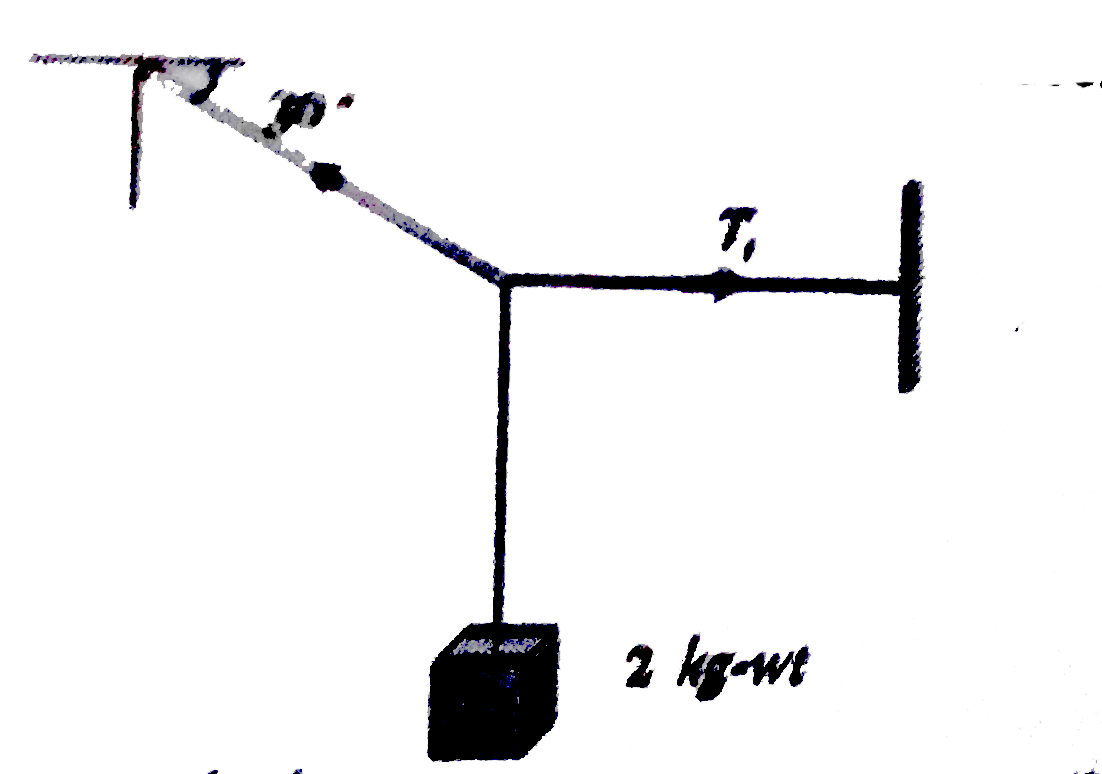 View Solution
View SolutionA uniform rod of length l and mass M is suspended on two vertical inextensible string as shown in figure. Then tension T in the left string at the instant, when right string snaps is?
 View Solution
View Solution