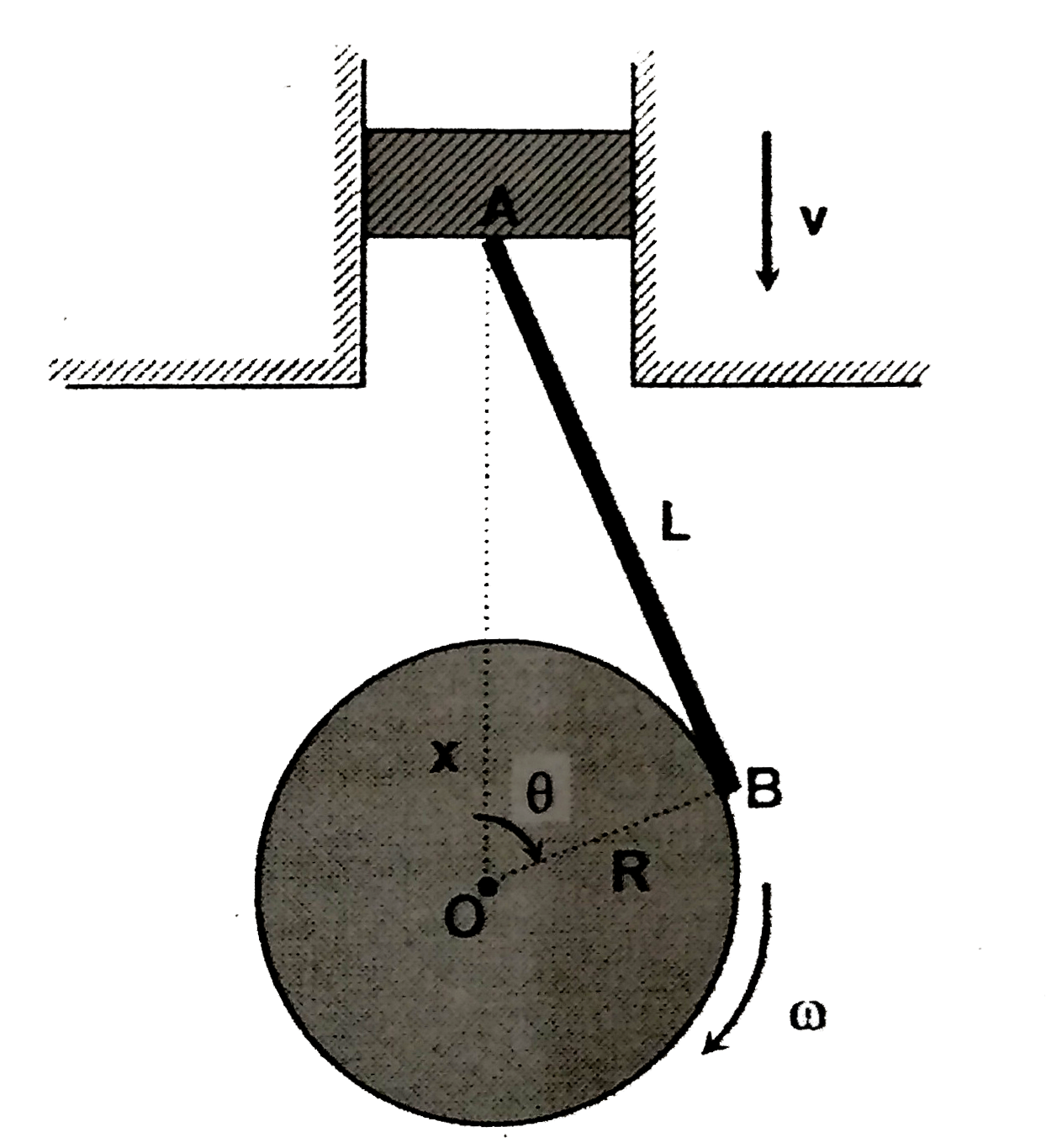
Find velocity of piston A in the given situation if angular velocity of wheel of radius R is ω (constant) in the clockwise sense (O is fixed point)
xRωsinθRcosθ+x
x2ωsinθRcosθ−x
xRωsinθRcosθ−x
R2ωsinθRcosθ−x
The correct Answer is:C
cosθ=x2+R2−L22xR⇒2xRcosθ=x2+R2+L2
2R{−xsinθ(dθdt)+cosθ(dxdt)}=2xdxdt
xv=Rvcosθ−Rxωsinθ
⇒v=(xRωsinθRcosθ−x)
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Suggest a method to locate IC for the following situations:
(a) Given the velocity of a point on the body and the angular velocity of the body.
(b) Given the lines of action of two nonparallel velocities. (c) Given the magnitude and direction of two parallel velocities.View SolutionTwo cylindrical hollow drums of radii Rand2R, and of a commom height h, are rotating with angular velocities ω (anti-clockwise) and ω (clockwise), respectively. Their axes, fixed are parallel and in a horizontal plane separated by (3R+δ). They are now brought in contact (δ→0).
(a) Show the frictional forces just after contact.
(b) Identify forces and torque external to the system just after contact.
(c ) What would be the ratio of final angular velocities when friction ceases ?View Solution
Knowledge Check
- Question 1 - Select One
If V is the velocity of the wave and ω is the angular velocity then the propagation constant (K) of the wave is given by
AK=VωBK=ωVCK=2πnDK=λ2π - Question 2 - Select One
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6 - Question 3 - Select One
A sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
Aat the bottom of the sphereBat the top of the sphereCat the centre of the sphereDanywhere inside the sphere
In figure, what be the sign of the velocity of the point P', which is the projection of the velocity of the reference particle P.P is moving in a circle of radius R in anti-clockwise direction.
 View Solution
View SolutionTwo particle 'A' and 'B' are moving on the same circle with angular ω1 and ω2 respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when,
(i) their sense of rotations is same,
(ii) and their sense of rotation is opposite.
 View Solution
View SolutionIn each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At t=0 (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and ω0 and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.
 View Solution
View SolutionIn the figure shown 'R' is a fixed conducting fixed ring of negligible resistance and radius 'a' PQ is a uniform rod of resistance r. It is hinged at the centre of the ring and rotated about this point in clockwise direction with a uniform angular velocity w. These is a uniform magnetic filled of strength 'B' ponting inwards. 'r' is a stationary resistance
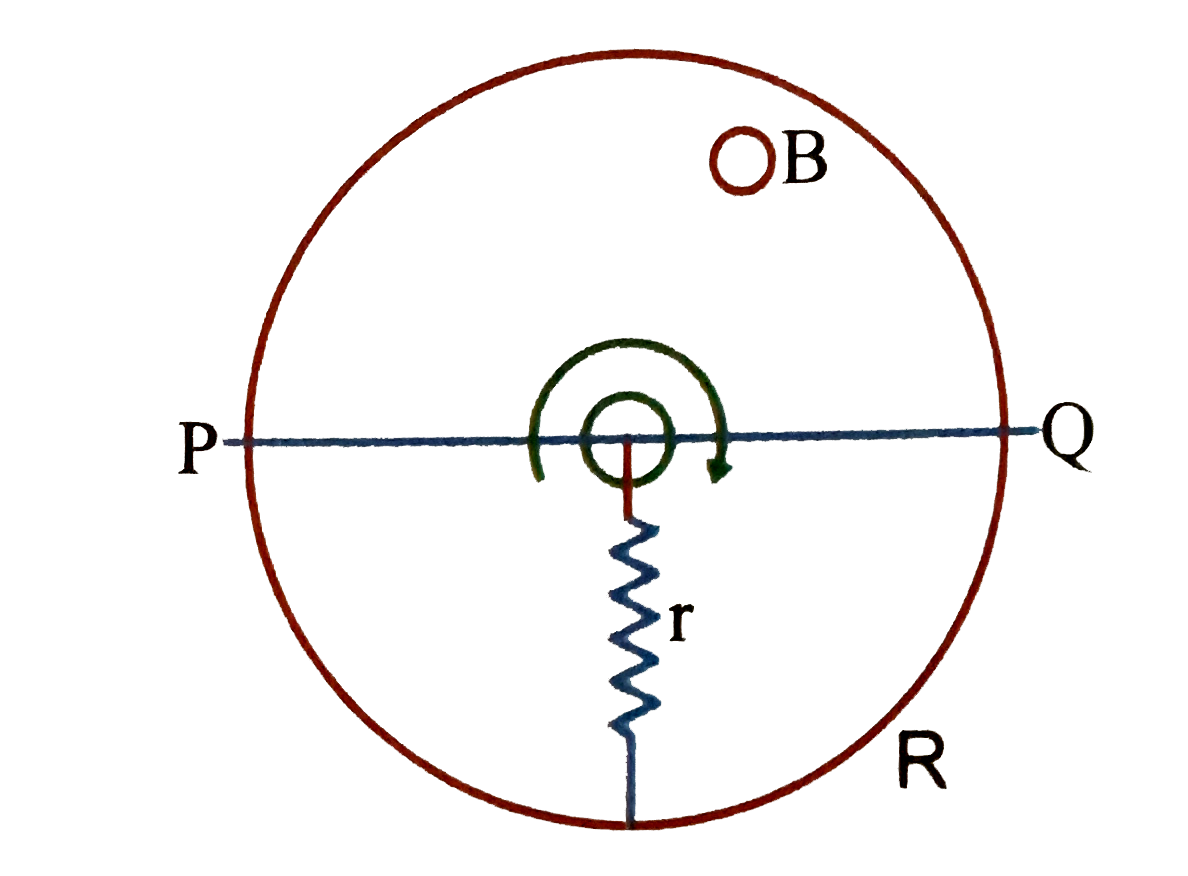 View Solution
View SolutionA disk is fixed at its centre O and rotating with constant angular velocity ω. There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30∘ with the vertical the ring is found to have a velocity v in the upward direction. Find ω of the disk. Given that the point A is R/2 distance above point O and length of the rod Ab is l
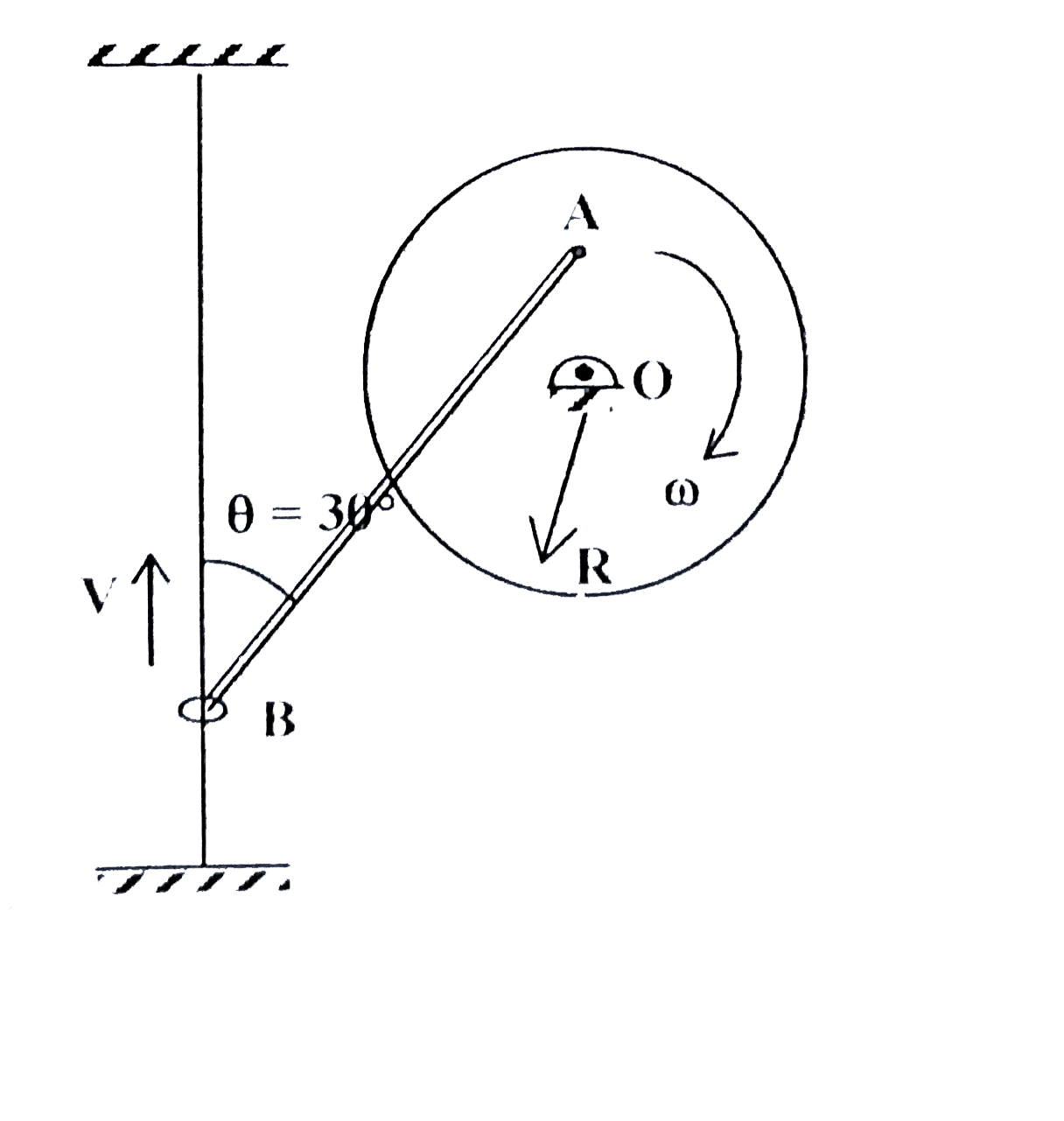 View Solution
View Solution

