An infinitely long cylinderical wire of radius R is carrying a current with current density $j = α r^{3}$ (where $α$ is constant and r is the distance from the axis of the wire). If the magnetic fixed at $r = \frac{R}{2}$ is $B_{1}$ and at r=2R is $B_{2}$ then the ratio $\frac{B_{2}}{B_{1}}$ is

A

2

B

4

C

6

D

8

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

When $r \leq R$
$B 2 π r = μ_{0} r \int 0 j 2 π r d r$
$B r = \frac{μ_{0} α r^{5}}{5}$
$B = \frac{μ_{0} α r^{4}}{5}, r \leq R$
when $r > R$
$B 2 π r = μ_{0} R \int 0 j 2 π r d r$
$B r = μ_{0} R \int 0 α r^{3} r d r$
$B r = \frac{μ_{0} α R^{5}}{5}$
$∴ B = \frac{μ_{0} α R^{5}}{5 r}, r > R$
at $r = \frac{R}{2}, B_{1} = \frac{μ_{0} α R^{4}}{80}$
at $r = 2 R, B_{2} = \frac{μ_{0} α R^{4}}{10}$
$∴ \frac{B_{2}}{B_{1}} = 8$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density $J = α r$ where a is a constant. Find the magnetic field for inside and outside prints.

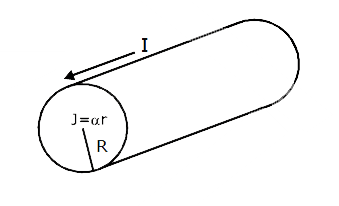AInside $\frac{α u_{0}}{3} r^{2}$
BOutside $\frac{α u_{0}}{3 R} r^{3}$
Cinside the outer conductor $\frac{α μ_{0}}{3} R^{2}$
DOutside $\frac{α μ_{0}}{3 r} R^{3}$
Question 2 - Select One

A time varying magnetic field $B = k r t$ (where k is a constant r is the radial distance from centre O) is existing in a circular region of radius R as shown. If induced electric field at $r = \frac{R}{2}$ is $E_{1}$ and at r=2R is $E_{2}$ then the ratio $\frac{E_{2}}{E_{1}}$ is
A6
B4
C2
D1
Question 3 - Select One
An infinite cylindrical wire of radius R and having current density varying with its radius r as, $J = J_{0} [1 - (r / R)]$ . Then answer the following questions.

Position where magnetic field strength is maximum.
AR
B $3 R / 4$
C $r / 2$
D $R / 4$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile