A small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius a√32 is :

(ga)1/2
(2ga)1/2
(3g2a)1/2
(3ga)1/2
The correct Answer is:B
A small bead …………….
Nsinθ=mg
Ncosθ=mω2a√32

When friction in absent :
∴Tanθ=2gω2a√3=13
ω=(2ga)12
Similar Questions
A small 100g sleeve B can slide on a smooth, circular and rigid wire frame A of radius 5m placéd in vertical plane. The wire frame is rotating about its vertical diameter at 2rads. When the sleeve is brought at a particular angular position other than the bottom and the top of the ring, the sleeve will not slide on the wire frame. What is force of interaction (in N) between the sleeve and the wire frame at this position?
'(##CEN_KSR_PHY_JEE_C07_020_Q11##)'View SolutionA bead slides on a frictoinless strainght rod fixed between points A and B of a vertical circular loop of radius as shown in the figure. Line BC is a vertical diameter. Denoting acceleration due to gravity by g, which of the following is correct expression for the time taken by the bead to slide from A to B
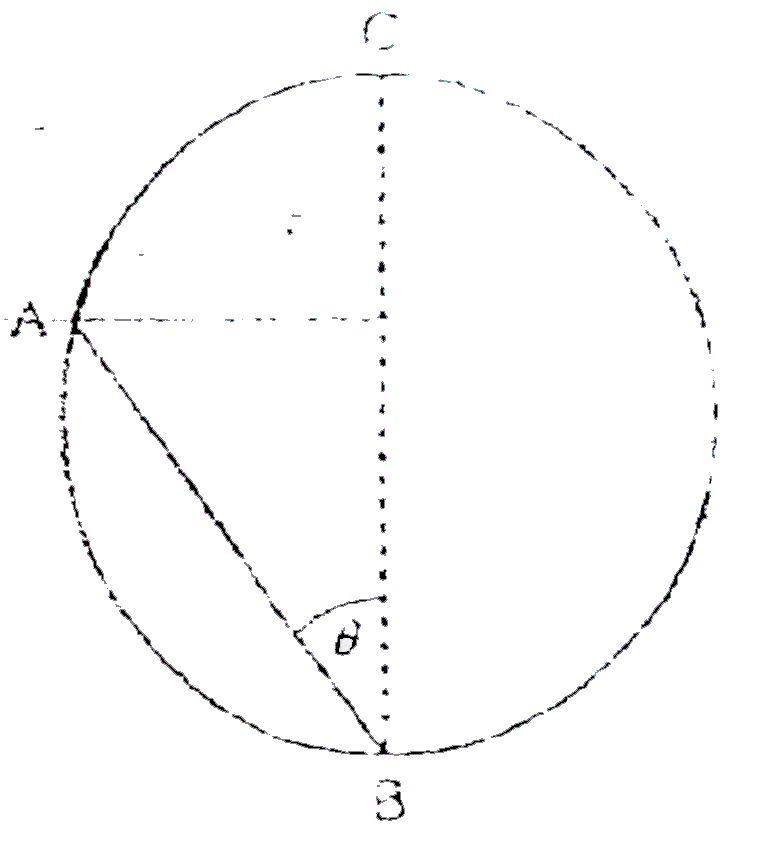 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A satellite of mass 'm' is revolving in an orbit of radius 2 R. The minimum energy required to lift it into another orbit of radius 3R is
(R is radius of the earth and g is acceleration due to gravity on its surface. )AgRm4BgRm8CgRm12DgRm18 - Question 2 - Select One
A particle of mass m performs vertical motion in a circle of radius r. Its potential energy at the highest point is ….. ( g is acceleration due to gravity)
A2 mgrBmgrC0D3 mgr - Question 3 - Select One
A smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is at rest w.r.t. the circular ring in the position shown. then ω2 is equal to:
 A2gaB2ga√3Cg√3aD2ag√3
A2gaB2ga√3Cg√3aD2ag√3
A small bead of mass m is carried by a circular hoop having center at O and radius √2m which rotates about a fixed vertical axis. The coefficient of friction between beed and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop. (g=10m/s2)
 View Solution
View SolutionA small disc can slide in a circular path on a frictionless inclined plane inclined at an angle of 30∘ with the help of a thread as shown. Mass of the disc is m and acceleration due to gravity is g. If the disc is released, when the thread is horizontal, expression for the tension in the thread at the lowest point is
 View Solution
View SolutionA bead is moving on a frictionless fixed circular wire of radius 0.8 m in horizontal plane with constant speed & there is no interaction force between bead & wire & it is also connected with string & spring .
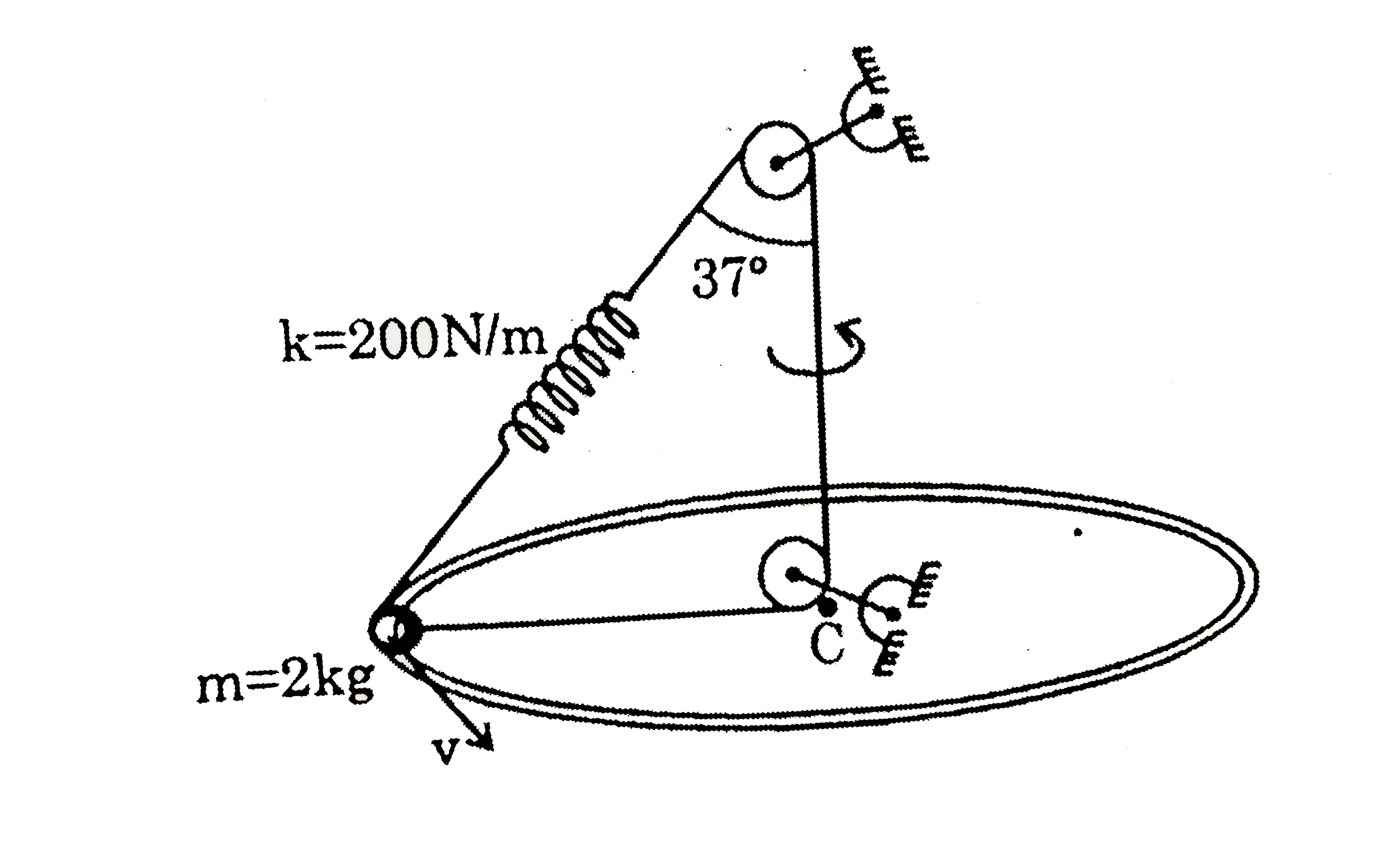 View Solution
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 View Solution
View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
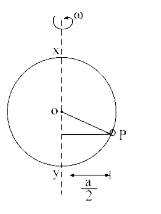 View Solution
View Solution

