Question

Let $M(2,\frac{13}{8})$ is the circumcentre of $\Delta PQR$ whose sides $PQ\text{and}PR$ are represented by the straight lines $4x-3y=0\text{and}4x+y=16$ respectively. The orthocentre of $\Delta PQR$ is

Options

A. area of `DeltaABC` equals `4`
B. area of `DeltaABC` equals `2`
C. coordinates of point `A` is `((3)/(2),2)`
D. coordinates of point `C` is `((7)/(2), 2)`

Answer

B::C::D

Explanation

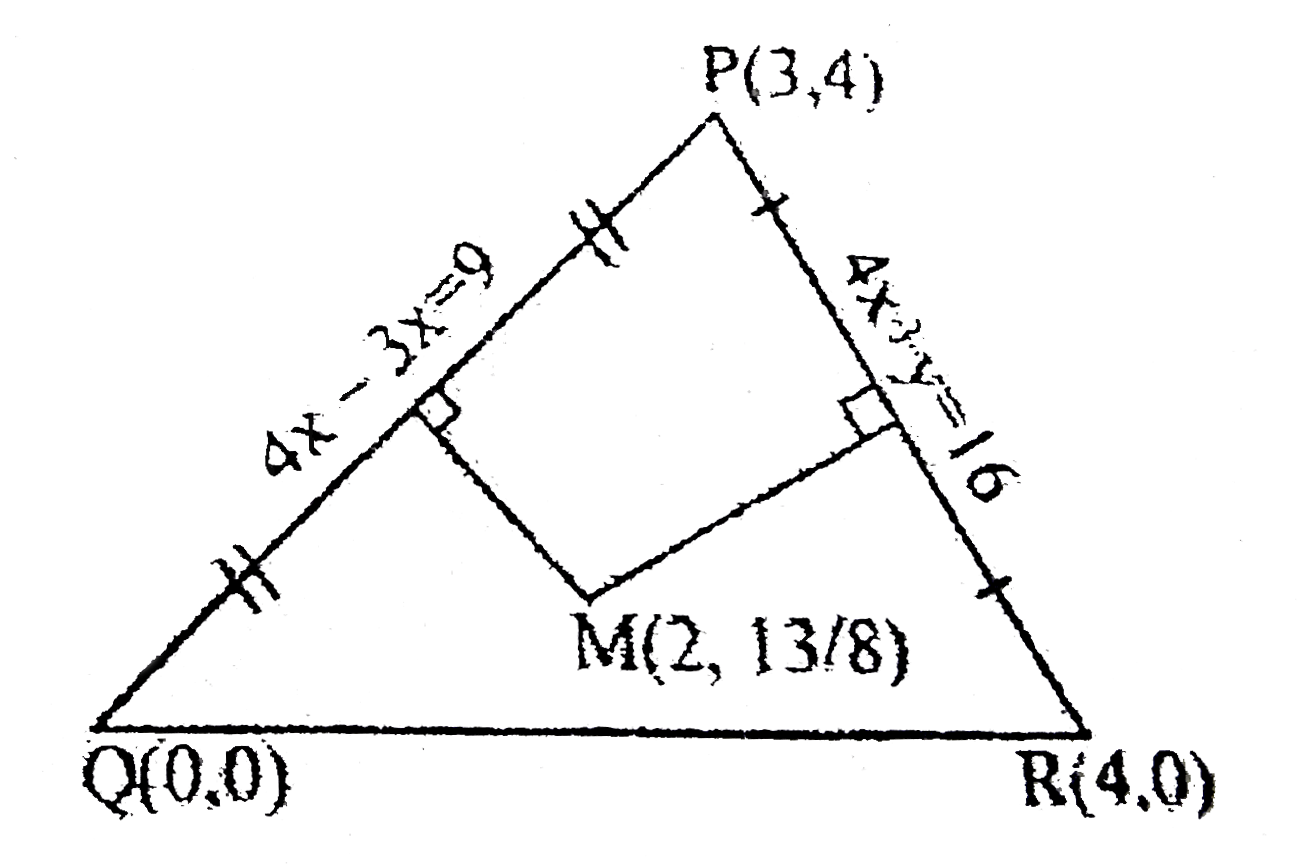
On solving `4x - 3y = 0` and `4x + y = 16`, we get `P(3,4)`.
The equation of lines perpendicular to `PQ` is `3x + 4y = k`
As above line passes through `M(2, (13)/(8))`
So `3(2) + 4((13)/(8)) = k rArr k = (25)/(2)`
`:.` Equation of `AM` is `3x + 4y = (25)/(2)`
Similarly, the equation of line perpendicular to
`PR` is `x - 4y = lambda`
As above line passes through `M(2, (13)/(8))`,
So `2 - 4((13)/(8)) = lambda rArr lambda = -(9)/(2)`
`:.` Equation of `CM` is `x - 4y = -(9)/(2)`
Now, on solving `4x - 3y = 0` and `3x + 4y = (25)/(2)`,
We get `A((3)/(2),2)`
Also on solving `4x + y = 16` and `x - 4y = -(9)/(2)`,
we get `C((7)/(2),2)`
As `A` is midpoint of `PQ`, so `Q = (0,0)` and `C` is the midpoint of `PR`, so `R = (4, 0)`
We have `(DeltaABC) = (1)/(2)||{:((3)/(2),2,1),(2,0,1),((7)/(2),2,1):}||=2` square units

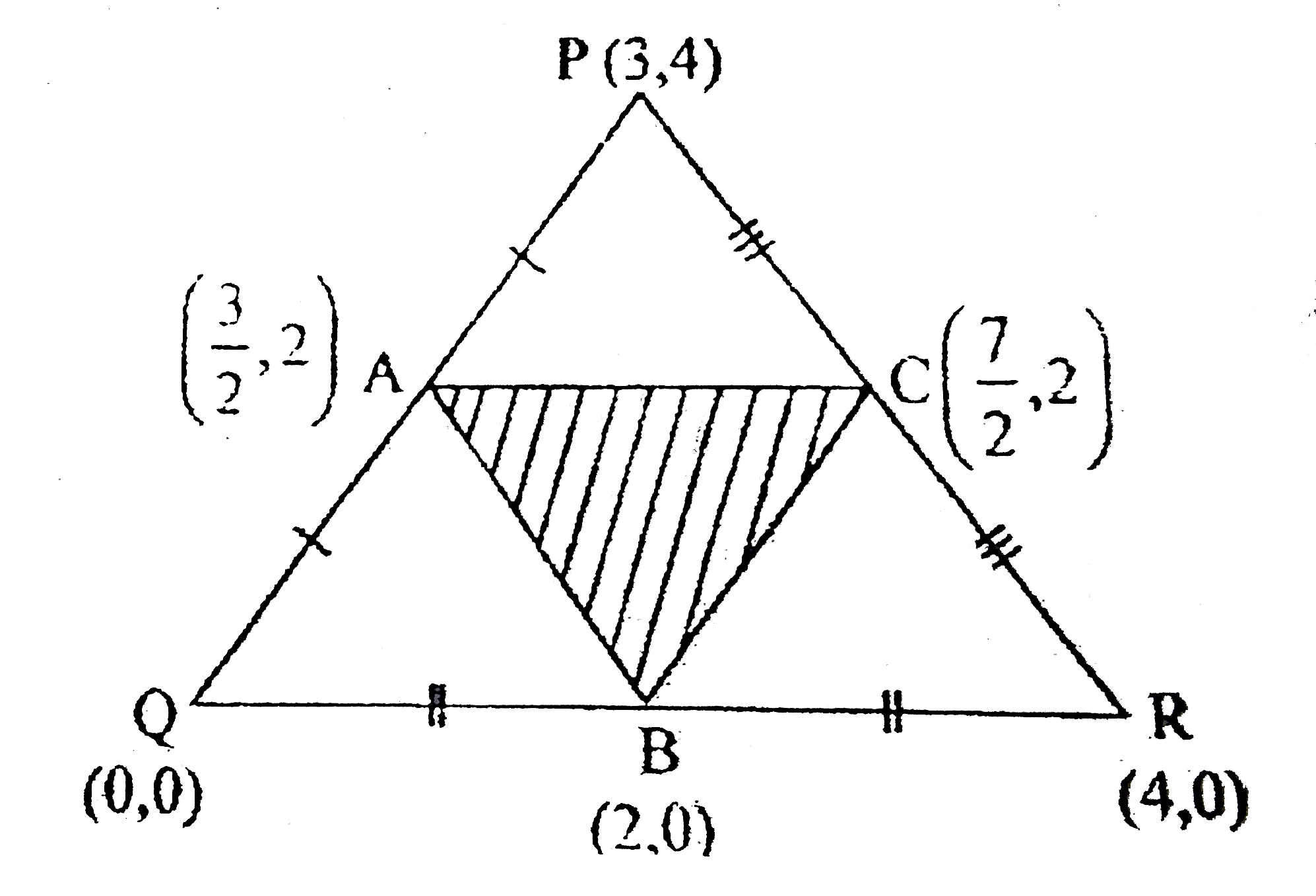
Aliter: area `(DeltaABC) = (1)/(4)` area `(DeltaPQR)`
`= (1)/(4) xx ((1)/(2) xx 4 xx 4) = 2` sq. units