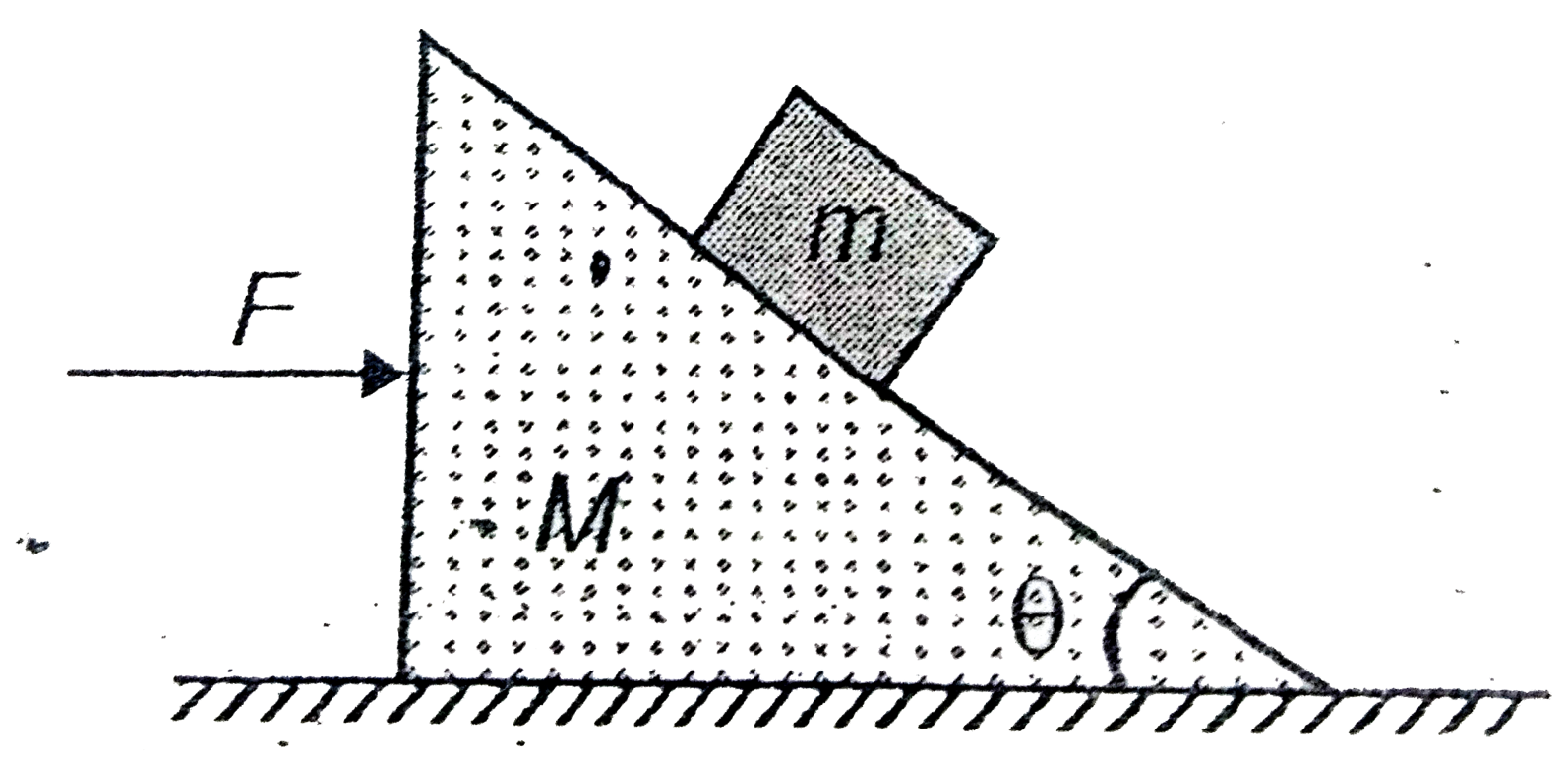
A block of mass m is placed on a wedge of mass M and a force F is acting on it as shown . If all surface are smooth , find the force F such that , there is no relative motion between m and M .

Since block and wedge both move together , they can be assumed as a system .
 ,
,
Let a be the common acceleration
∴F=(M+m)a … (A)
Now draw FBD of block m
In inertial f.o.r (Ground )

Nsinθ=ma ...(i)
Ncosθ=mg ...(ii)
From (i) and (ii)
a=tanθ
Putting the value of a in equation (A)
F=(M+m)gtanθ
In Non - inertial f.o.r. (Wedge)

∑F×=0
⇒Nsinθ−ma=0 ....(i)
∑Fy=0⇒Ncosθ−mg=0 ....(ii) '
This yields the same set of equations and the same result i.e F = (M+m)gtanθ
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Illustration
Explore 5 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:TRY YOURSELF
Explore 67 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
A smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
 AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m
AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than mAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θA block of mass m lies on wedge of mass M , which lies on fixed horizontal surface. The wedge is free to move on the horizontal surface. A horizontal force of magnitude F is applied on block as shown neglecting friction at all surface, the value of force F such that block has no relative motion w.r.t wedge will be: (Where g is acceleration due to gravity)
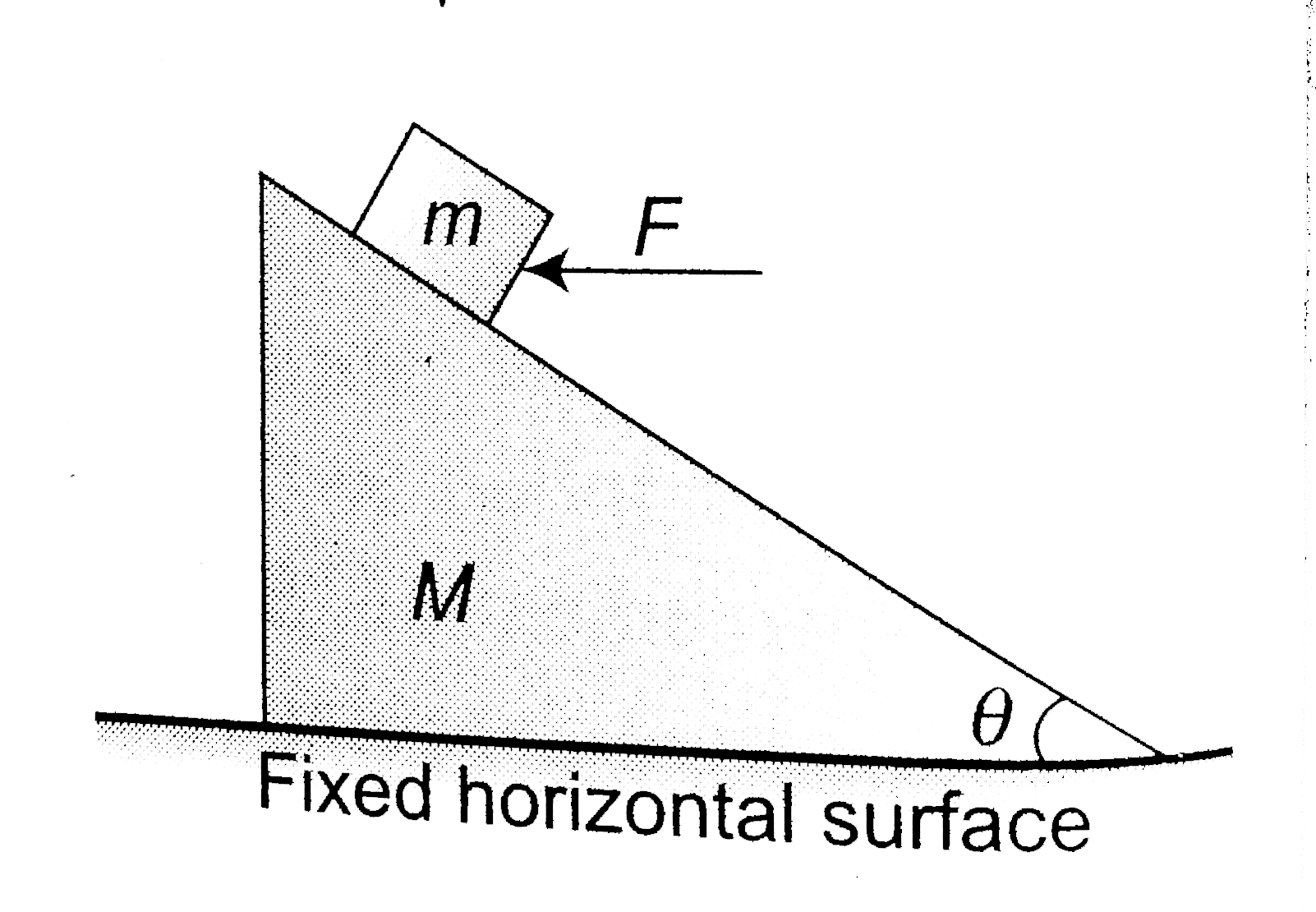 A(M+m)gtanθB(M+m)gcotθCmM(M+m)gtanθDmM(M+m)gcosθ
A(M+m)gtanθB(M+m)gcotθCmM(M+m)gtanθDmM(M+m)gcosθ
Two smooth wedges of equal mass m are placed as shown in figure. All surfaces are smooth. Find the velocities of A & B when A hits the ground.
View SolutionA block of mass m, is kept on a wedge of mass M, as shown in figure such that mass m remains stationary w.r.t. wedge. The magnitude of force P is

View SolutionA block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View SolutionThe mass m is placed on a body of mass M. There is no friction. The force F is applied on M on it moves with acceleration a. Then, the force on the top body is
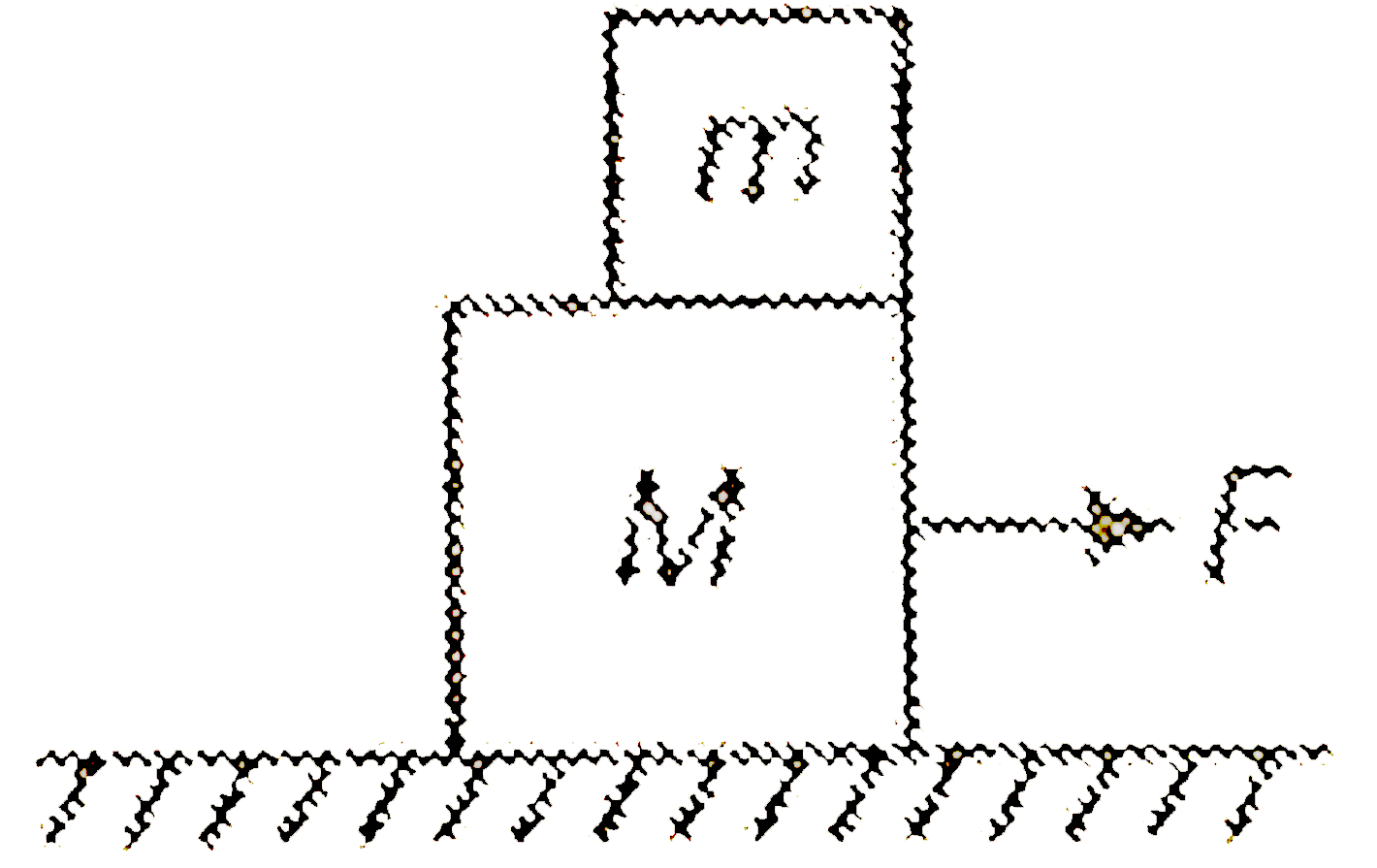
View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View Solution
