The equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
Step by step video & image solution for The equations of bisectors of two lines L_1 & L_2 are 2x-16y-5=0 and 64x+ 8y+35=0. lf the line L_1 passes through (-11, 4), the equation of acute angle bisector of L_1 & L_2 is: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let L1:3X+4Y−1=0andL2:5z−12y+2=0 be two given lines. Let image of every point on L1 w.r.t a line L lies on L2 then possible equation of 'L' can be
View SolutionThe straight line L≡X+Y+1=0andL1≡X+2Y+3=0 are intersectiong, m is the slope of the straight line L2 such that L is the bisector of the angle between L1andL2 The value of m2 is .
View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Name or write equations for the lines L1 and L2
View SolutionThe vector equations of two lines L1andL2 are respectively, L1:r=2i+9j+13k+λ(i+2j+3k)andL2:r=−3i+7j+pk+μ(−i+2j−3k) Then, the lines L1andL2 are
View SolutionThe bisector of two lines L and L are given by 3x2−8xy−3y2+10x+20y−25=0. If the line L1 passes through origin, find the equation of line L2.
View SolutionGiven equation of line L1 is y=4
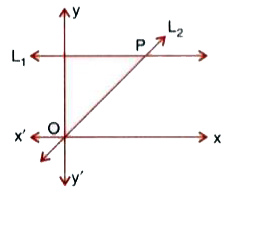
Write the slope of line L1 if L2 is the bisector of angle O.
View SolutionGiven equation of line L1 is y=4

Find the equation of L2.
View SolutionThe line l1x+m1y+n=0andl2x+m2y+n=0 will cut the coordinate axes at concyclic points if (A) l1m1=l2m2 (B) l1m2=l2m1 (C) l1l2=m1m2 (D) l1l2m1m2=n2
View Solution
