Two strings A and B of equal lenth but un equal linear mass density are tied together with a knot and stretched between two supports. A particular frquency happens to produce a standing wave on each part, with node at the knot as shown. If linear mass density of the two strings A and B are μ1 and μ2 respectively, then
μ1=μ1
μ1<μ2
μ1>μ2
can't be decided
The correct Answer is:C
f1=f2
D1<D2
C=fD
∴C1<C2
but C=√Tμ
∴Mu1>μ2
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Two strings, A and B, of lengths 4L and L respectively and same mass M each, are tied together to form a knot 'O' and stretched under the same tension. A transverse wave puise is sent along the composite string from the side A, as shown to the right. Which of the following diagrams correctly shows the reflected and transmitted waves pulses near the knot 'O' ?
_S01_011_Q01.png)
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View Solution
Knowledge Check
- Question 1 - Select One
Two strings, A and B, of lengths 4L and L respectively and same mass M each, are tied together to form a knot 'O' and stretched under the same tension. A transverse wave puise is sent along the composite string from the side A, as shown to the right. Which of the following diagrams correctly shows the reflected and transmitted waves pulses near the knot 'O' ?
A_S01_011_O01.png)
B_S01_011_O02.png)
C_S01_011_O03.png)
D_S01_011_O04.png)
- Question 2 - Select One
If equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
Ad1d2(d1+d2)B2d1d2(d1+d2)Cd1d22(d1+d2)D(d1+d2)2 - Question 3 - Select One
Two quantities A and B are related by A/B=m where m is linear mass density and A is force. The dimensions of B will be same as that of-
APressureBWorkCMomentumDLatent heat
Two long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View SolutionTwo long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
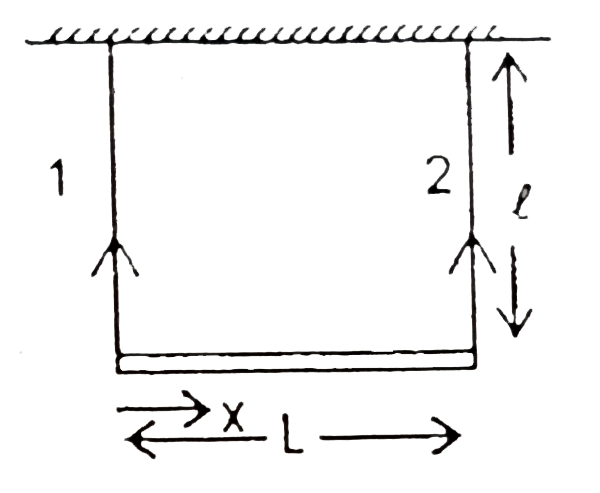
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionString I and II have identical and linear mass densities, but string I is under greater tension than string II. The accompanying figure shows four different situations, A to D, in which standing wave patterns exist on the two strings. In which situation it is possible that strings I and II are oscillating at the same resonant frequency ?
View Solution