If equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
d1d2(d1+d2)
2d1d2(d1+d2)
d1d22(d1+d2)
(d1+d2)2
The correct Answer is:B
To find the density of a mixture of two liquids with equal masses and different densities d1 and d2, we can follow these steps:
Step 1: Define the masses and densities
Let the mass of each liquid be m. The densities of the two liquids are given as:
- Density of liquid 1: d1
- Density of liquid 2: d2
Step 2: Calculate the volumes of the liquids
Using the formula for density, we can express the volumes of the two liquids in terms of their masses and densities:
- Volume of liquid 1, V1=md1
- Volume of liquid 2, V2=md2
Step 3: Calculate the total mass and total volume of the mixture
The total mass of the mixture is the sum of the masses of the two liquids:
- Total mass, Mtotal=m+m=2m
The total volume of the mixture is the sum of the volumes of the two liquids:
- Total volume, Vtotal=V1+V2=md1+md2
Step 4: Express the total volume in a single fraction
To combine the volumes, we can find a common denominator:
Vtotal=md1+md2=m(1d1+1d2)=m(d1+d2d1d2)
Step 5: Calculate the density of the mixture
The density of the mixture d can be calculated using the formula:
d=MtotalVtotal=2mVtotal
Substituting the expression for Vtotal:
d=2mm(1d1+1d2)=21d1+1d2
Step 6: Simplify the expression
We can simplify this further:
d=2d1+d2d1d2=2d1d2d1+d2
Final Result
Thus, the density of the mixture of the two liquids is:
d=2d1d2d1+d2
---
Let the mass of each liquid be m. The densities of the two liquids are given as:
- Density of liquid 1: d1
- Density of liquid 2: d2
Using the formula for density, we can express the volumes of the two liquids in terms of their masses and densities:
- Volume of liquid 1, V1=md1
- Volume of liquid 2, V2=md2
The total mass of the mixture is the sum of the masses of the two liquids:
- Total mass, Mtotal=m+m=2m
- Total volume, Vtotal=V1+V2=md1+md2
To combine the volumes, we can find a common denominator:
Vtotal=md1+md2=m(1d1+1d2)=m(d1+d2d1d2)
The density of the mixture d can be calculated using the formula:
d=MtotalVtotal=2mVtotal
Substituting the expression for Vtotal:
d=2mm(1d1+1d2)=21d1+1d2
We can simplify this further:
d=2d1+d2d1d2=2d1d2d1+d2
Thus, the density of the mixture of the two liquids is:
d=2d1d2d1+d2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - C
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - D
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Equal masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionTwo substances of densities ρ1 and ρ2 are mixed in equal volume and the relative density of mixture is 4. When they are mixed in equal masses, the relative density of the mixture is 3. the values of ρ1 and ρ2 are:
View SolutionTwo cylinders of same cross-section and length L but made of two different materials of densities d1 and d2 are cemented together to from a cylinder of length 2L. The combination floats in a liquid of density d d1<d2 then
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
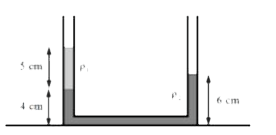
View SolutionWhen two substances of specific gravities d1 and d2 are mixed in equal volumes the specific garvity of mixture is found to be ρ1. When they are mixed in equal masses, the specific gravity of the mixture is found to be ρ2.(d1≠d2)
View SolutionAn object is put one by one in three liquids having different densities. The object floats with 19,211and37 parts of their volumes outside the liquid surface in liquids of densities d1,d2andd3, respectively. Which of the following statement is correct ?
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View Solution
